When all coefficients of ![]() and
and ![]() are real (implying that
are real (implying that
![]() is the transfer function of
a real filter), it will
always happen that the complex one-pole filters will occur in
complex conjugate pairs. Let
is the transfer function of
a real filter), it will
always happen that the complex one-pole filters will occur in
complex conjugate pairs. Let ![]() denote any one-pole
section in the PFE of Eq.(6.7). Then if
denote any one-pole
section in the PFE of Eq.(6.7). Then if ![]() is complex and
is complex and ![]() describes a real filter, we will also find
describes a real filter, we will also find
![]() somewhere among
the terms in the one-pole expansion. These two terms can be paired to
form a real second-order section as follows:
somewhere among
the terms in the one-pole expansion. These two terms can be paired to
form a real second-order section as follows:
![\begin{eqnarray*}
H(z) &=& \frac{r}{1-pz^{-1}} + \frac{\overline{r}}{1-\overline{p}z^{-1}}\\ [5pt]
&=& \frac{r-r\overline{p}z^{-1}+\overline{r}-\overline{r}pz^{-1}}{(1-pz^{-1})(1-\overline{p}z^{-1})}\\ [5pt]
&=&
\frac{2\mbox{re}\left\{r\right\}-2\mbox{re}\left\{r\overline{p}\right\}z^{-1}}{1-2\mbox{re}\left\{p\right\}z^{-1}+ \left\vert p\right\vert^2 z^{-2}}
\end{eqnarray*}](img711.png)
Expressing the pole ![]() in polar form as
in polar form as
![]() ,
and the residue as
,
and the residue as
![]() ,
the last expression above can be rewritten as
,
the last expression above can be rewritten as

The use of polar-form coefficients is discussed further in the section on two-pole filters (§B.1.3).
Expanding a transfer function into a sum of second-order terms with
real coefficients gives us the filter coefficients for a parallel bank
of real second-order filter sections. (Of course, each real pole can
be implemented in its own real one-pole section in parallel with the
other sections.) In view of the foregoing, we may conclude that every
real filter with ![]() can be implemented as a parallel bank
of biquads.7.6 However, the full generality of a biquad
section (two poles and two zeros) is not needed because the PFE
requires only one zero per second-order term.
can be implemented as a parallel bank
of biquads.7.6 However, the full generality of a biquad
section (two poles and two zeros) is not needed because the PFE
requires only one zero per second-order term.
To see why we must stipulate ![]() in Eq.(6.7), consider the sum of two
first-order terms by direct calculation:
in Eq.(6.7), consider the sum of two
first-order terms by direct calculation:
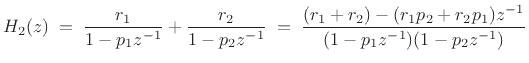 |
(7.9) |