Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
To illustrate an example involving complex poles, consider the filter
where 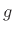 can be any real or complex value. (When
can be any real or complex value. (When 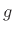 is real, the
filter as a whole is real also.) The poles are then
is real, the
filter as a whole is real also.) The poles are then 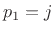 and
and
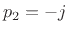 (or vice versa), and the factored form can be written as
(or vice versa), and the factored form can be written as
Using Eq.(6.8), the residues are found to be
Thus,
More examples are given in §3.12.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]