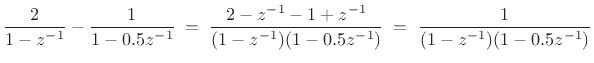Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Consider the two-pole filter
The poles are 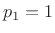 and
and 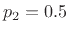 . The corresponding residues are then
. The corresponding residues are then
We thus conclude that
As a check, we can add the two one-pole terms above to get
as expected.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
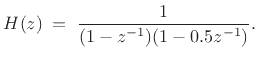
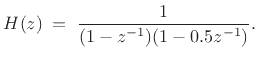
![\begin{eqnarray*}
r_1 &=& \left.(1-z^{-1})H(z)\right\vert _{z=1}
\eqsp \left.\frac{1-z^{-1}}{(1-z^{-1})(1-0.5z^{-1})}\right\vert _{z=1} \\
&=& \left.\frac{1}{1-0.5z^{-1}}\right\vert _{z=1}
\eqsp 2\,,\mbox{ and}\\ [10pt]
r_2 &=& \left.(1-0.5z^{-1})H(z)\right\vert _{z=0.5}
\eqsp \left.\frac{1-0.5z^{-1}}{(1-z^{-1})(1-0.5z^{-1})}\right\vert _{z=0.5} \\
&=& \left.\frac{1}{1-z^{-1}}\right\vert _{z=0.5}
\eqsp -1\,.
\end{eqnarray*}](img699.png)