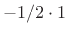Converting Signal Flow Graphs to State-Space Form by Hand

The procedure of the previous section quickly converts any transfer function to state-space form (specifically, controller canonical form). When the starting point is instead a signal flow graph, it is usually easier to go directly to state-space form by labeling each delay-element output as a state variable and writing out the state-space equations by inspection of the flow graph.

For the example of the previous section, suppose we are given Eq.$\,$(G.14) in direct-form II (DF-II), as shown in Fig.G.1. It is important that the filter representation be canonical with respect to delay, i.e., that the number of delay elements equals the order of the filter. Then the third step (writing down controller canonical form by inspection) may replaced by the following more general procedure:

1. Assign a state variable to the output of each delay element (indicated in Fig.G.1).
2. Write down the state-space representation by inspection of the flow graph.

Figure: Direct-form-II representation of the difference equation in Eq.$\,$(G.7), after pulling out the direct path as given in Equations (G.14-G.15).

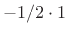The state-space description of the difference equation in Eq.$\,$(G.7) is given by Eq.$\,$(G.16). We see that controller canonical form follows immediately from the direct-form-II digital filter realization, which is fundamentally an all-pole filter followed by an all-zero (FIR) filter (see §9.1.2). By starting instead from the transposed direct-form-II (TDF-II) structure, the observer canonical form is obtained [28, p. 87]. This is because the zeros effectively precede the poles in a TDF-II realization, so that they may introduce nulls in the input spectrum, but they cannot cancel output from the poles (e.g., from initial conditions). Since the other two digital-filter direct forms (DF-I and TDF-I--see Chapter 9 for details) are not canonical with respect to delay, they are not used as a basis for deriving state-space models.