Complex Resonator

Normally when we need a resonator, we think immediately of the two-pole resonator. However, there is also a complex one-pole resonator having the transfer function

$$H(z) = \frac{g}{1-pz^{-1}} \protect$$ (B.6)

where $p=Re^{j\theta_c}$ is the single complex pole, and $g$ is a scale factor. In the time domain, the complex one-pole resonator is implemented as

$$y(n) = g x(n) + p y(n-1).$$

Since $p$ is complex, the output $y(n)$ is generally complex even when the input $x(n)$ is real.

Since the impulse response is the inverse z transform of the transfer function, we can write down the impulse response of the complex one-pole resonator by recognizing Eq.(B.6) as the closed-form sum of an infinite geometric series, yielding

$$h(n) = u(n) g p^n,$$

where, as always, $u(n)$ denotes the unit step function:

$$u(n) \isdef \left\{\begin{array}{ll} 1, & n\geq 0 \\ [5pt] 0, & n<0 \\ \end{array} \right.$$

Thus, the impulse response is simply a scale factor $g$ times the geometric sequence $p^n$ with the pole $p$ as its ``term ratio''. In general, $p^n = R^n e^{j\omega_c nT}$ is a sampled, exponentially decaying sinusoid at radian frequency $\omega_c=\theta_c/T$ . By setting $p$ somewhere on the unit circle to get

$$p \isdef e^{j\omega_c T},$$

we obtain a complex sinusoidal oscillator at radian frequency $\omega_c$ rad/sec. If we like, we can extract the real and imaginary parts separately to create both a sine-wave and a cosine-wave output:

$$\begin{eqnarray*} \mbox{re}\left\{h(n)\right\} &=& u(n) g \cos(\omega_c n T)\\ \mbox{im}\left\{h(n)\right\} &=& u(n) g \sin(\omega_c n T) \end{eqnarray*}$$

These may be called phase-quadrature sinusoids, since their phases differ by 90 degrees. The phase quadrature relationship for two sinusoids means that they can be regarded as the real and imaginary parts of a complex sinusoid.

By allowing $g$ to be complex,

$$g \isdef A e^{j\phi}$$

we can arbitrarily set both the amplitude and phase of this phase-quadrature oscillator:

$$\begin{eqnarray*} \mbox{re}\left\{h(n)\right\} &=& u(n) A \cos(\omega_c n T + \phi)\\ \mbox{im}\left\{h(n)\right\} &=& u(n) A \sin(\omega_c n T + \phi) \end{eqnarray*}$$

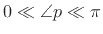
The frequency response of the complex one-pole resonator differs from that of the two-pole real resonator in that the resonance occurs only for one positive or negative frequency $\omega_c$ , but not both. As a result, the resonance frequency $\omega_c$ is also the frequency where the peak-gain occurs; this is only true in general for the complex one-pole resonator. In particular, the peak gain of a real two-pole filter does not occur exactly at resonance, except when $\theta_c \isdef \omega_c T = 0$ , $\pi/2$ , or $\pi$ . See §B.6 for more on peak-gain versus resonance-gain (and how to normalize them in practice).