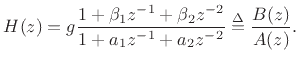
The general biquad transfer function was given in Eq.(B.8) to be
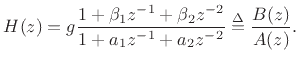
To specialize this to a second-order unity-gain allpass filter, we require
It is easy to show that, given any monic denominator polynomial
Thus, to obtain an allpass biquad section, the numerator polynomial is simply the ``flip'' of the denominator polynomial. To obtain unity gain, we set
In terms of the poles and zeros of a filter
![]() , an
allpass filter must have a zero at
, an
allpass filter must have a zero at ![]() for each pole at
for each pole at ![]() .
That is if the denominator
.
That is if the denominator ![]() satisfies
satisfies ![]() , then the
numerator polynomial
, then the
numerator polynomial ![]() must satisfy
must satisfy ![]() . (Show this in
the one-pole case.) Therefore, defining
. (Show this in
the one-pole case.) Therefore, defining
![]() takes care of
this property for all roots of
takes care of
this property for all roots of ![]() (all poles). However, since we
prefer that
(all poles). However, since we
prefer that ![]() be a polynomial in
be a polynomial in ![]() , we define
, we define
![]() , where
, where ![]() is the order of
is the order of ![]() (the number of poles).
(the number of poles).
![]() is then the flip of
is then the flip of ![]() .
.
For further discussion and examples of allpass filters (including muli-input, multi-output allpass filters), see Appendix C. Analog allpass filters are defined and discussed in §E.8.