Typically, ![]() , i.e., the number of frequency constraints is much
greater than the number of design variables (filter taps). In these
cases, we have an overdetermined system of equations (more
equations than unknowns). Therefore, we cannot generally satisfy all
the equations, and we are left with minimizing some error criterion to
find the ``optimal compromise'' solution.
, i.e., the number of frequency constraints is much
greater than the number of design variables (filter taps). In these
cases, we have an overdetermined system of equations (more
equations than unknowns). Therefore, we cannot generally satisfy all
the equations, and we are left with minimizing some error criterion to
find the ``optimal compromise'' solution.
In the case of least-squares approximation, we are minimizing the
Euclidean distance, which suggests the following geometrical
interpretation:
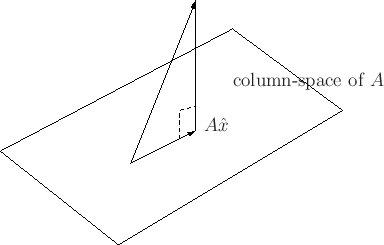
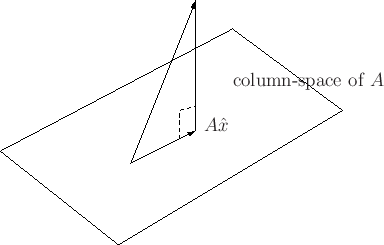
This diagram suggests that the error vector
![]() is orthogonal to
the column space of the matrix
is orthogonal to
the column space of the matrix ![]() , hence it must be orthogonal to each
column in
, hence it must be orthogonal to each
column in ![]() .
.
This is how the orthogonality principle can be used to derive the fact that the best least squares solution is given by
Note that the pseudo-inverse ![]() projects the vector
projects the vector ![]() onto the column space of
onto the column space of ![]() .
.
In Matlab: