Least Squares Optimization

$$\hat{x} \mathrel{\stackrel{\Delta}{=}}\arg \min_x \left\Vert\,Ax-b\,\right\Vert _2 = \arg \min_x \left\Vert\,Ax-b\,\right\Vert _2^2$$

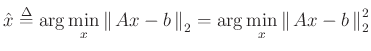
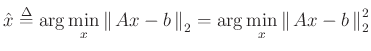
Hence we can minimize

$$\left\Vert\,Ax-b\,\right\Vert _2^2 = (Ax-b)^T(Ax-b)$$

Expanding this, we have:

$$(Ax-b)^T(Ax-b) = (b^T-x^TA^T)(Ax-b)$$

This is quadratic in $x$ , hence it has a global minimum which we can find by taking the derivative, setting it to zero, and solving for $x$ . Doing this yields:

$$A^TAx-A^Tb=0$$

These are the famous normal equations whose solution is given by:

$$\zbox{\hat{x} = \left[(A^TA)^{-1}A^T\right]b}$$

The matrix

$$A^\dagger \isdef (A^TA)^{-1}A^T$$

is known as the pseudo-inverse of the matrix $A$ .