Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Plan:
- Fix the bilinear-transform frequency-scaling parameter
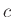 once for the whole system (so there is only one frequency-warping)
once for the whole system (so there is only one frequency-warping)
- Set the ``connector'' wave impedance
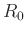 separately for each
circuit element to eliminate the delay-free path in its reflectance
separately for each
circuit element to eliminate the delay-free path in its reflectance
- We will then get scattering when we connect different elements
together
This yields the following elementary reflectances:
The original element values remain only in the waveguide-interface
impedances
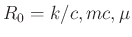
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download WaveDigitalFilters.pdf
Download WaveDigitalFilters_2up.pdf
Download WaveDigitalFilters_4up.pdf

![]()