Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Given:
Find:
such that:
Solving for 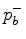 is not immediate because
is not immediate because
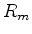 depends on
depends on
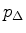 which depends on
which depends on 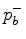 .
.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download SingleReeds.pdf
Download SingleReeds_2up.pdf
Download SingleReeds_4up.pdf


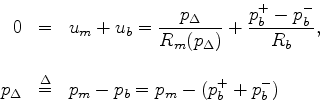
![]() is not immediate because
is not immediate because
![]() depends on
depends on
![]() which depends on
which depends on ![]() .
.