Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Pre-solve the graphical intersection and store the result in a
look-up table
Let 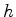 denote half-pressure
denote half-pressure 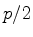 . Then
. Then
Subtracting both sides from 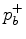 and solving for
and solving for 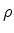 gives
Now, for each
gives
Now, for each
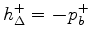 , find
, find
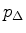 graphically, and store the
resulting reflection coefficient
graphically, and store the
resulting reflection coefficient
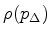 as a function of
as a function of
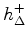 :
:
Then the real-time reed computation reduces simply to
This is the form chosen for implementation above
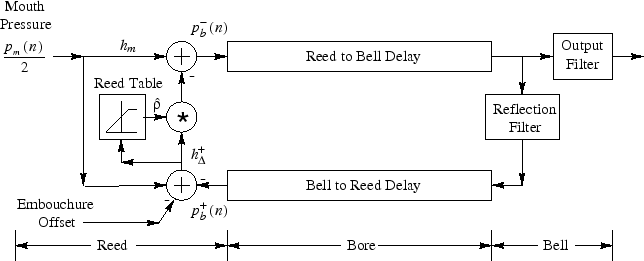
Table-Reduced Reed Reflection Coefficient
- Control variable = mouth half-pressure

-
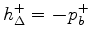 computed from incoming bore pressure by a subtraction
computed from incoming bore pressure by a subtraction
- Table is indexed by
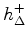
- Result of lookup is multiplied by
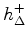
- Result of multiplication is subtracted from

- Total reed cost = two subtractions, one multiply,
and one table lookup per sample
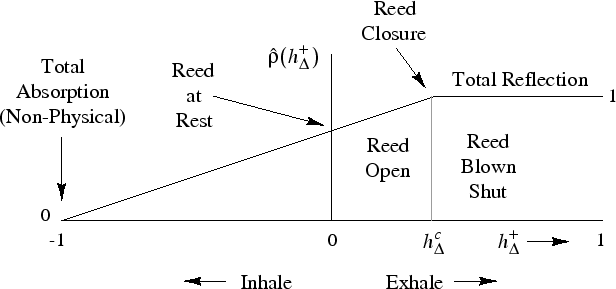
Simple Piecewise-Linear Reed Table
- Corner point
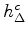 = smallest pressure difference giving reed closure
= smallest pressure difference giving reed closure
- In fixed-point,
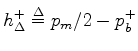 is confined to
is confined to 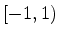
- Embouchure and reed-stiffness set by
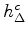 and slope
and slope 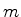 [
[
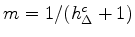 in the figure]
in the figure]
- Zero at maximum negative pressure
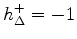 is not physical but is practical for inhibiting overflow
is not physical but is practical for inhibiting overflow
- A brighter tone is obtained by increasing the curvature as the reed
begins to open [E.g.,
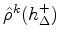 , for
, for 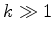 ]
]
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download SingleReeds.pdf
Download SingleReeds_2up.pdf
Download SingleReeds_4up.pdf
![]() denote half-pressure
denote half-pressure ![]() . Then
. Then
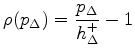
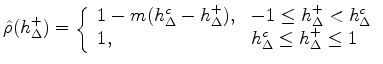
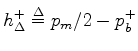 is confined to
is confined to