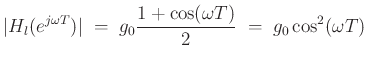Length 3 FIR Loop Filter with Variable DC Gain

Relaxing the unity-dc-gain restriction, but keeping linear phase, we have

$$H_l(z) = b_0 + b_1 z^{-1}+ b_0 z^{-2}$$   (linear phase)

We can use the remaining two degrees of freedom for brightness $B$ & sustain $S$ :

$$\begin{eqnarray*} g_0 &\mathrel{\stackrel{\mathrm{\Delta}}{=}}& e^{-6.91 P / S} \\ [5pt] b_0 &=& g_0 (1 - B)/4 = b_2 \\ b_1 &=& g_0 (1 + B)/2 \end{eqnarray*}$$

where

$$\begin{eqnarray*} P &=& \hbox{period in seconds (total loop delay)} \\ S &=& \hbox{desired sustain time in seconds} \\ B &=& \hbox{brightness parameter in the interval $[0,1]$} \end{eqnarray*}$$

Sustain time $S$ is defined here as the time to decay $60$ dB (or $6.91$ time-constants) when brightness $B$ is maximum ($B=1$ ). At minimum brightness ($B=0$ ), we have

$$\vert H_l(e^{j\omega T})\vert \;=\;g_0\frac{1 + \cos(\omega T)}{2} \;=\;g_0 \cos^2(\omega T)$$