Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
- Start with a pole at dc (digital integrator):
- Move it from radius 1 to radius 0.9 using
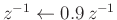 :
:
- Now progress from radius 0.9 to
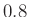 using
using
with
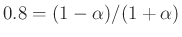
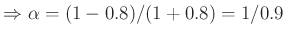 :
:
Desired Pole Radius
Pole radius 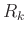 and
and  are related by
are related by
The ideal loss filter  therefore satisfies
therefore satisfies
The desired delay-line filters are therefore
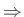
or
Now use invfreqz or stmcb, etc., in Matlab to design
low-order filters 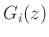 for each delay line.
for each delay line.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Reverb.pdf
Download Reverb_2up.pdf
Download Reverb_4up.pdf
![$\displaystyle H(z) = \frac{1}{1-z^{-1}} \;\leftrightarrow\;[1,1,1,\ldots]
$](img105.png)
![$\displaystyle H(z) = \frac{1}{1-0.9\,z^{-1}} \;\leftrightarrow\;[1,\,0.9,\,0.81,\,\ldots]
$](img121.png)
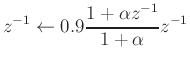
![\begin{eqnarray*}
H(z) &=& \frac{1}{1-0.9\,\frac{1+\alpha z^{-1}}{1+\alpha}z^{-1}}
\;=\;\frac{1}{1-0.9\,\frac{0.9+z^{-1}}{0.9+1}z^{-1}}\\ [10pt]
&=& \frac{1}{1-\frac{0.81}{1.9}z^{-1}+ \frac{1}{1.9}z^{-2}}
\end{eqnarray*}](img126.png)
![$\displaystyle H(z) = \frac{1}{1-z^{-1}} \;\leftrightarrow\;[1,1,1,\ldots]
$](img105.png)
![$\displaystyle H(z) = \frac{1}{1-0.9\,z^{-1}} \;\leftrightarrow\;[1,\,0.9,\,0.81,\,\ldots]
$](img121.png)
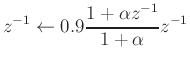
![\begin{eqnarray*}
H(z) &=& \frac{1}{1-0.9\,\frac{1+\alpha z^{-1}}{1+\alpha}z^{-1}}
\;=\;\frac{1}{1-0.9\,\frac{0.9+z^{-1}}{0.9+1}z^{-1}}\\ [10pt]
&=& \frac{1}{1-\frac{0.81}{1.9}z^{-1}+ \frac{1}{1.9}z^{-2}}
\end{eqnarray*}](img126.png)
![]() and
and ![]() are related by
are related by
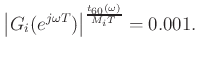
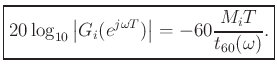
![]() for each delay line.
for each delay line.