Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
We have
The string displacement is updated in time by three
matrix-vector products, plus a forcing term
![$ {\bf g}
f_n({\bf y}_{n-1}[i_h],y^h(n-1))$](img30.png) :
:
- The length
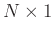 matrix
matrix 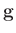 represents the
shape of the hammer excitation over the length of the string.
The nonzero elements correspond to the width of the hammer relative to
that of the string. For greatest accuracy, it should be time varying,
but it may be approximated by a constant shape.
represents the
shape of the hammer excitation over the length of the string.
The nonzero elements correspond to the width of the hammer relative to
that of the string. For greatest accuracy, it should be time varying,
but it may be approximated by a constant shape.
- The element
![$ {\bf y}_n[i_h]$](img33.png) is the string displacement sample
closest to the hammer position.
is the string displacement sample
closest to the hammer position.
- The scalar function
 denotes hammer position
at time
denotes hammer position
at time 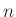 .
.
- The scalar function
![$ f_n({\bf y}_{n}[i_h],y^h_n)$](img35.png) sets the
amplitude of the hammer force distribution across position at time
sets the
amplitude of the hammer force distribution across position at time
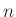 .
.
- The force exerted on the string by the hammer is a nonlinear
function of the hammer-string separation
![$ y^h_n - {\bf y}_{n}[i_h]$](img36.png) .
.
- The time evolution of the hammer
must be computed numerically by a separate finite difference scheme.
Typical models include a classical point mass, a
nonlinear spring (which gets stiffer when compressed), and
a very small amount of damping.
Note that the FDS involves 3 steps of ``lookback.'' It turns out this
model goes unstable in the limit as the sampling rate goes to
infinity!
- There is no problem at any normal audio sampling rate--the
sampling rate must be on the order of hundreds of megahertz to trigger
the instability.
- The model can be stabilized at all sampling rates by
using instead a two-time-step scheme.
- Watch for forthcoming publications by Stefan Bilbao at CCRMA.
- We'll talk about stability of finite difference schemes later.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Download PianoString.pdf
Download PianoString_2up.pdf
Download PianoString_4up.pdf
![]() :
: