Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
- Convergence: Since the approximations to the second derivatives
we used were second order accurate (in
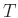 and
and 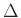 ), the scheme
as a whole is accurate as
), the scheme
as a whole is accurate as
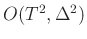 .
.
- Making an FDS more accurate (i.e., converge faster) generally requires a
recursion involving more grid variables.
- An FDS for a higher order PDE also generally involves more grid variables.
- From a signal processing point of view, a more accurate
simulation of an LTI medium is obtained by increasing the order
of the filter.
- Note that an optimal filter design yields FDS coefficients which
may be translated back to differential equation coefficients (which
may or may not have physical meaning).
- Stability becomes more difficult to ensure in general (need to check
eigenvalue magnitudes). The addition of boundary conditions makes this
even more difficult.
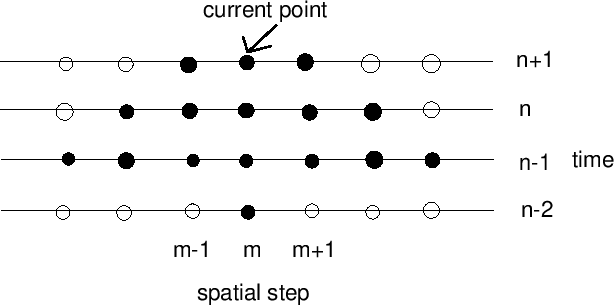
- A good finite difference scheme may not be explicit, and
hence may require matrix inversions (generally sparse).
For example, the dependence diagram below represents an implicit scheme: We cannot calculate the grid variables at the
current timestep as weighted sums of grid variables at previous
instants.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download NumericalInt.pdf
Download NumericalInt_2up.pdf
Download NumericalInt_4up.pdf