Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The matrix
can be called the state transition matrix corresponding to the
state-space description determined by the choice of state vector
and the state update can be written more simply in vector form as
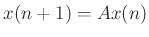 . Note that the state-space description is
indexed by frequency
. Note that the state-space description is
indexed by frequency 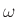 , regarded as fixed.
, regarded as fixed.
- From linear systems theory, we know that such a system
will be asymptotically stable if the eigenvalues
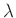 of
the matrix
of
the matrix 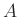 are both less than 1 in magnitude.
are both less than 1 in magnitude.
- It is easy to show that the eigenvalues of
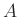 are
are
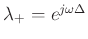 and
and
 . Thus,
. Thus,
 .
.
- While we are not guaranteed asymptotic stability,
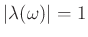 does imply that, in some sense, our solution
is not getting larger with time at any spatial
frequency. This can be defined as marginal stability.
does imply that, in some sense, our solution
is not getting larger with time at any spatial
frequency. This can be defined as marginal stability.
- Note that we should expect the eigenvalues to have unit modulus,
because the wave equation we started with corresponds to a
lossless medium (an ideal gas). The original PDEs were
derived without any loss mechanisms.
- A lossless discrete-time simulation can be highly desirable,
particularly as a modeling starting point.
- This kind of ``Von Neumann analysis'' can be applied
to any constant-coefficient FDS which is linear in its spatial
directions.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download NumericalInt.pdf
Download NumericalInt_2up.pdf
Download NumericalInt_4up.pdf
![$\displaystyle A \mathrel{\stackrel{\mathrm{\Delta}}{=}}\left[\begin{array}{cc} 2\cos\omega\Delta & -1 \\ [2pt] 1 & 0 \end{array}\right]
$](img85.png)
![$\displaystyle A \mathrel{\stackrel{\mathrm{\Delta}}{=}}\left[\begin{array}{cc} 2\cos\omega\Delta & -1 \\ [2pt] 1 & 0 \end{array}\right]
$](img85.png)
![$\displaystyle {\boldmath {x}}(n) \mathrel{\stackrel{\mathrm{\Delta}}{=}}\left[\begin{array}{c} U^{n}(\omega) \\ [2pt] U^{n-1}(\omega) \end{array}\right]
$](img86.png)