Finite Differences: Some basics

Suppose we begin with the simplest possible differential equation, that relating current and voltage in an inductor:

$$\begin{eqnarray*} v(t)=L\frac{di}{dt} \end{eqnarray*}$$

We assume that one of the quantities, say $i$ is provided by some source. We need to discretize this continuous time equation. First sample $i$ at regular intervals $nT$ (in the simplest case), to obtain a sequence $i_{n}$, and assume that we will be obtaining a voltage sequence $v_{n}$ from it. There are many ways of approximating the differentiation operator;

• set $\frac{di}{dt}\simeq (i_{n}-i_{n-1})/T$. This yields the equation:
  $$\begin{eqnarray*} v_{n}=(L/T)(i_{n}-i_{n-1}) \end{eqnarray*}$$
  

  This is probably the simplest way of discretizing a derivative, and is called a backwards difference.

• a slightly more sophisticated discretization involves rewriting the equation for the inductor in the following way:
  $$\begin{eqnarray*} i(t)=\frac{1}{L}\left(\int_{0}^{t}v(t')dt'\right) + i_{0} \end{eqnarray*}$$
  

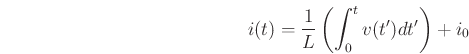
  and thus

  $$\begin{eqnarray*} i(nT) &=& \frac{1}{L}\left(\int_{0}^{nT}v(t')dt'\right) + i_{0... ...T\right) +\frac{T}{2L}\left(v\left((n-1)T\right) + v(nT)\right) \end{eqnarray*}$$
  

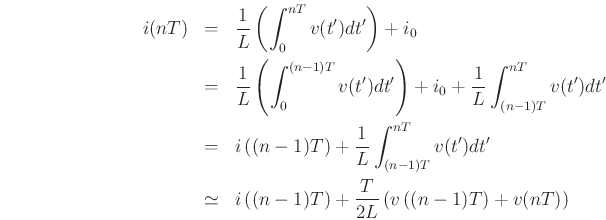
  yielding the scheme:

  $$\begin{eqnarray*} v_{n}=-v_{n-1}+\frac{2L}{T}(i_{n}-i_{n-1}) \end{eqnarray*}$$
  

• This is called the trapezoid rule of numerical integration (or differentiation), and it can be seen as the basis for the WDF approach to filtering and numerical integration.

• There are many other ways of performing this discretization; in general we can imagine writing a general scheme:
  $$\begin{eqnarray*} \sum_{k=0}^{\infty}a_{k}v_{n-k}=\sum_{k=0}^{\infty}b_{k}i_{n-k} \end{eqnarray*}$$
  

  which in some sense behaves like the original continuous time equation.