Accuracy

Suppose we take the backward-difference approximation $v_{n}=(L/T)(i_{n}-i_{n-1})$ , and expand $i_{n-1}$ in Taylor series about $i_{n}$ . This yields:

$$\begin{eqnarray*} v_{n} &=& (L/T)\left(i_{n}-\left(i_{n}-T\left.\frac{di}{dt}\right\vert _{nT} + O(T^{2})\right)\right) \\ &=& \left. L\frac{di}{dt}\right\vert _{nT} + O(T) \end{eqnarray*}$$

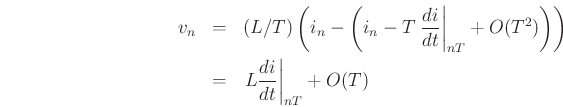
So the difference scheme approximates the continuous time equation to an accuracy that depends on $T$ , the step size. Thus we expect that the discretization will do a better job as $T$ gets small.

Performing the same analysis for the trapezoid rule yields:

$$\begin{eqnarray*} v_{n} &=& L\left.\frac{di}{dt}\right\vert _{nT} + O(T^{2}) \end{eqnarray*}$$

So we say that the trapezoid rule is second-order accurate in $T$ .

• In general, the more accurate a difference scheme, the more information from neighboring grid points it will require.