More General Differential Equations

A more general linear constant coefficient differential equation can be written as:

$$\begin{eqnarray*} \sum_{k=0}^{N}a_{k}\frac{d^{k}v}{dt^{k}}=\sum_{k=0}^{M}b_{k}\frac{d^{k}i}{dt^{k}} \end{eqnarray*}$$

or, in the frequency domain, assuming zero initial conditions,

$$\sum_{k=0}^{N}a_{k}s^k V(s)=\sum_{k=0}^{M}b_{k}s^k I(s)$$

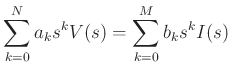
We can define a transfer-function relationship as follows:

$$\begin{eqnarray*} Z(s) \mathrel{\stackrel{\mathrm{\Delta}}{=}}\frac{V(s)}{I(s)} ... ...s^2 + \cdots + b_M s^M} {1 + a_1 s + a_2 s^2 + \cdots + a_N s^N} \end{eqnarray*}$$

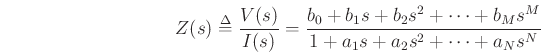
where we have normalized $a_0\neq 0$ to $1$. Note that $Z(s)$ is a rational function of $s$ of order $\max(N,M)$.

If $i(t)$ and $v(t)$ are measured at the same point, then $Z(s)$ is a driving point impedance, as depicted below:

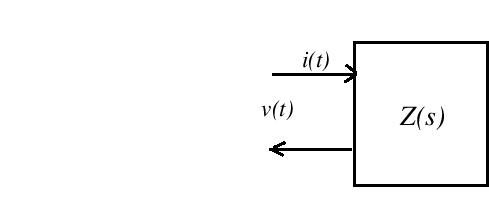
If the circuit (or mechanical system) is physically passive, then $Z(s)$ must be positive real.