Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Rewriting as a first-order system in the stresses and velocities
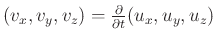 gives
gives
with
- Symmetric hyperbolic even if
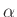 ,
, 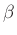 ,
, 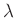 and
and 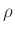 are spatially varying.
are spatially varying.
- Coupling of time derivatives (this does not occur in the other systems seen so far). Thus a scalar staggered grid is out of the question (need
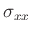 ,
,
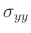 and
and
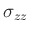 at same grid point, at same time step).
at same grid point, at same time step).
Fix: vectorized differences.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Meshes.pdf
Download Meshes_2up.pdf
Download Meshes_4up.pdf
![]() gives
gives