Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
We will now analyze the filter bank interpretation of the STFT with
hop size set to 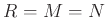 .
.
The kth subband signal in the DFT filter bank can be written as:
with
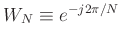 .
The signal
.
The signal 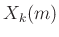 is regarded as a complex sequence formed from the
is regarded as a complex sequence formed from the
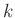 th DFT bin over time
th DFT bin over time 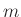 (in frames).
(in frames).
Making the change of variable 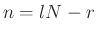 , the above equation becomes:
, the above equation becomes:
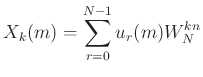 |
(11) |
with
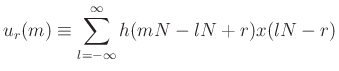 |
(12) |
Therefore, (![[*]](../icons/crossref.png) ) can be interpreted as computing a
length-
) can be interpreted as computing a
length-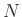 FFT applied to the input block
FFT applied to the input block
![$ [u_0(m) \cdots u_{N-1}(m)]^T$](img393.png) .
.
Now, we'll form a simpler representation of the sequence 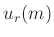 .
First, define the polyphase decomposition of
.
First, define the polyphase decomposition of 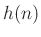 and
and 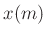 :
:
If the filter 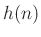 has length
has length 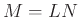 , then each of its polyphase
components
, then each of its polyphase
components 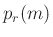 has length
has length 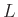 .
Now define the sequence
.
Now define the sequence 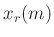
Finally, (![[*]](../icons/crossref.png) ) can be expressed as:
) can be expressed as:
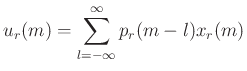 |
(13) |
Thus, every input bin to the DFT is actually a convolution between
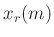 and
and 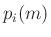 , the
, the 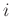 th polyphase filter of the lowpass
prototype filter,
th polyphase filter of the lowpass
prototype filter, 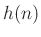 .
.
- Complexity is now the cost of one full-rate convolution with
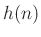 and the FFT cost.
and the FFT cost.
- If
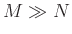 (
(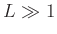 ), we can keep aliasing error within tolerable limits.
), we can keep aliasing error within tolerable limits.
- If
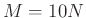 (
(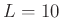 ), it is possible to keep the reconstruction error
below 0.1%.
), it is possible to keep the reconstruction error
below 0.1%.
- Similar development for the synthesis DFT bank
- Notice that when the polyphase filters are scalars (1-tap FIR filters)
of unit gain, then this is simply a DFT block transform, with a
rectangular window. The frequency response is a sinc, with poor
frequency characteristics.
- By extending the length of the polyphase filters,
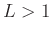 , then
the freqeuency characteristics of the window can become much better.
, then
the freqeuency characteristics of the window can become much better.
- The window length is no longer restricted to be of the same
length as the transform.
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download JFB.pdf
Download JFB_2up.pdf
Download JFB_4up.pdf
[Comment on this page via email]
![]() .
.

![]() , the above equation becomes:
, the above equation becomes:
![]() ) can be interpreted as computing a
length-
) can be interpreted as computing a
length-![]() FFT applied to the input block
FFT applied to the input block
![]() .
.
![]() .
First, define the polyphase decomposition of
.
First, define the polyphase decomposition of ![]() and
and ![]() :
:
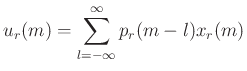
![]() and
and ![]() , the
, the ![]() th polyphase filter of the lowpass
prototype filter,
th polyphase filter of the lowpass
prototype filter, ![]() .
.