Supplementary: Optimal Least Squares Bandlimited Interpolation Formulated as a Fractional Delay Filter

Consider a filter which delays its input by $\Delta$ samples:

• Ideal impulse response = bandlimited delayed impulse = delayed sinc
  $$h_\Delta(t) \;=\;$$sinc$$(t-\Delta) \;\mathrel{\stackrel{\mathrm{\Delta}}{=}}\;\frac{\sin\left[\pi (t-\Delta)\right]}{\pi (t-\Delta)}$$

• Ideal frequency response = ``brick wall'' lowpass response, cutting off at $f_s/2$ and having linear phase $e^{-j\omega \Delta T}$
  $$\begin{eqnarray*} H_\Delta(\omega)&\mathrel{\stackrel{\mathrm{\Delta}}{=}}&\hbox{\sc FT}(h_\Delta) \;=\;\left\{\begin{array}{ll} e^{-j\omega \Delta}, & \vert\omega\vert<\pi f_s \\ [5pt] 0, & \vert\omega\vert\geq\pi f_s \\ \end{array} \right.\\ \rightarrow\quad H_\Delta(e^{j\omega T})&=& e^{-j\omega \Delta T}, \quad -\pi \leq \omega T<\pi\\ &\leftrightarrow& \mbox{sinc}(n-\Delta), \quad n=0,\pm 1, \pm 2, \ldots \end{eqnarray*}$$
  

  after critically sampling in the time domain.

The sinc function is an infinite-impulse-response (IIR) digital filter with no recursive form $\Rightarrow$ non-realizable.

To obtain a finite impulse response (FIR) interpolating filter, let's formulate a least-squares filter-design problem:

Desired Interpolator Frequency Response

$$H_\Delta \left(e^{j\omega T}\right)\;=\;e^{-j\omega \Delta T},\quad \Delta \;=\;\hbox{Desired delay in samples}$$

FIR Frequency Response, Zero-Phase Alignment

$${\hat H}_\Delta \left(e^{j\omega T}\right)\;=\;\sum_{n=-\frac{L-1}{2}}^\frac{L-1}{2} {{\hat h}_\Delta}(n) e^{-j\omega nT}$$

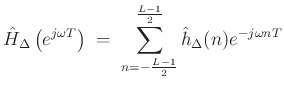
Error to Minimize

$$E\left(e^{j\omega T}\right)= H_\Delta \left(e^{j\omega T}\right)- {\hat H}_\Delta \left(e^{j\omega T}\right)$$

$\ensuremath{L_2}$ Error Norm

$$\begin{eqnarray*} J(\underline{h}) \mathrel{\stackrel{\mathrm{\Delta}}{=}}\left\Vert\,E\,\right\Vert _2^2 &=& \frac{T}{2\pi}\int_{-\pi/T}^{\pi/T} \left\vert E\left(e^{j\omega T}\right)\right\vert^2 d\omega \\ &=& \frac{T}{2\pi}\int_{-\pi/T}^{\pi/T} \left\vert H_\Delta \left(e^{j\omega T}\right)- {\hat H}_\Delta \left(e^{j\omega T}\right)\right\vert^2 d\omega \end{eqnarray*}$$

By Parseval's Theorem

$$J(\underline{h}) = \sum_{n=0}^\infty \left\vert h_\Delta (n) - {{\hat h}_\Delta}(n)\right\vert^2$$

Optimal Least-Squares FIR Interpolator

$${{\hat h}_\Delta}(n) = \left\{\begin{array}{ll} \mbox{sinc}(n-\Delta), & \frac{L-1}{2} \leq n \leq \frac{L-1}{2} \\ [5pt] 0, & \hbox{otherwise} \\ \end{array} \right.$$