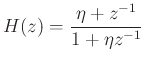Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Intuitively, ramping the coefficients of the allpass gradually
``grows'' or ``hides'' one sample of delay. This tells us how to
handle resets when crossing sample boundaries (sufficiently slowly).
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Interpolation.pdf
Download Interpolation_2up.pdf
Download Interpolation_4up.pdf
Visit the online book containing this material.
![\begin{eqnarray*}
{\hat x}(n-\Delta) \mathrel{\stackrel{\mathrm{\Delta}}{=}}y(n) &=& \eta \cdot x(n) + x(n-1) - \eta \cdot y(n-1) \\
&=& \eta \cdot \left[ x(n) - y(n-1)\right] + x(n-1)
\end{eqnarray*}](img23.png)
![\begin{eqnarray*}
{\hat x}(n-\Delta) \mathrel{\stackrel{\mathrm{\Delta}}{=}}y(n) &=& \eta \cdot x(n) + x(n-1) - \eta \cdot y(n-1) \\
&=& \eta \cdot \left[ x(n) - y(n-1)\right] + x(n-1)
\end{eqnarray*}](img23.png)