Centered Finite Difference

Backward Euler [ $s\leftarrow (1-z^{-1})/T)$ ] has a 1/2 sample delay at all frequencies, while Forward Euler [ $s\leftarrow(z-1)/T)$ ] has a 1/2 sample advance. We can eliminate this time-skew using a
centered finite difference:

$$\begin{eqnarray*} \hat{\dot v}(nT) &=& \frac{v_{n+1}-v_{n-1}}{2T}\\ [10pt] \Rightarrow\quad f_{n}&\approx&\frac{m}{2T}(v_{n+1}-v_{n-1})\\ [10pt] \Rightarrow\quad \hat{v}_{n+1} &=& \hat{v}_{n-1} + \frac{2T}{m}f_{n} \end{eqnarray*}$$

• No time delay or advance
• Compare the Leapfrog integrator
• $s$ to $z$ mapping is
  $$s \;=\;\frac{z-z^{-1}}{2T} \;\to\; \frac{e^{j\omega T}-e^{-j\omega T}}{2T} \;=\;j\frac{\sin(\omega T)}{T} \;\approx\;j\omega % s \eqsp \frac{z-\zi}{2T} \eqsp z\frac{1-\zmt}{2T} \;\to\; \ejoT\frac{1-e^{-j2\omega T}}{2T}$$
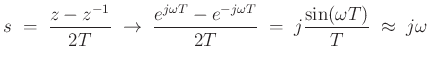
  at low frequencies, but note how it reaches a maximum at $\omega T=\pi/2$ and comes back down to 0 at $\omega T=\pi$