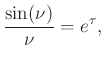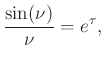Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The same argument can be extended to the entire right-half plane as
follows. Going back to
since
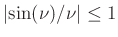 for all real
for all real 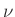 , and since
, and since
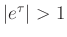 for
for 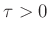 , this equation clearly has no solutions in
the right-half plane. Therefore,
, this equation clearly has no solutions in
the right-half plane. Therefore,
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download ConicalModeling.pdf
Download ConicalModeling_2up.pdf
Download ConicalModeling_4up.pdf