Stability Proof

First consider the roots of the denominator

$$D(s) = 2s - 1 + e^{-2s}.$$

At any pole (solution $s$ of $D(s)=0$ ), we must have

$$s = \frac{1-e^{-2s}}{2}$$

To obtain separate equations for the real and imaginary parts, take the real and imaginary parts of $D(\sigma+j\omega)=0$ to get

$$\begin{eqnarray*} \mbox{re}\left\{D(s)\right\} &=& (2\sigma - 1) + e^{-2\sigma}\cos(2\omega) = 0 \\ \mbox{im}\left\{D(s)\right\} &=& 2\omega - e^{-2\sigma}\sin(2\omega) = 0 \end{eqnarray*}$$

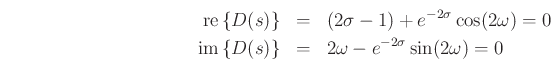
Both of these equations must hold at any pole of the reflectance. For stability, we further require $\sigma\leq 0$ . Defining $\tau = 2\sigma$ and $\nu=2\omega$ , we obtain the simpler conditions

$$\begin{eqnarray*} e^\tau ( 1 - \tau) &=& \cos(\nu) \\ e^\tau &=& \frac{\sin(\nu)}{\nu} \end{eqnarray*}$$

For any poles of $R_J(s)$ on the $j\omega$ axis, we have $\tau=0$ , and the second equation reduces to sinc$(\nu)=1$ . It is well known that the sinc function is less than $1$ in magnitude at all $\nu$ except $\nu=0$ . Therefore, this relation can hold only at $\omega=\nu=0$ , and so

$$\zbox{\hbox{\emph{Any right-half-plane poles occur at $\omega=0$.}}}$$