Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Since both of the conditions
are clearly satisfied for
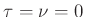 , we see that there is in fact a pole
in the reflectance at dc (
, we see that there is in fact a pole
in the reflectance at dc (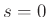 ), provided it is not canceled by a zero at dc
in the numerator
), provided it is not canceled by a zero at dc
in the numerator 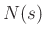 .
.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download ConicalModeling.pdf
Download ConicalModeling_2up.pdf
Download ConicalModeling_4up.pdf


![]() , we see that there is in fact a pole
in the reflectance at dc (
, we see that there is in fact a pole
in the reflectance at dc (![]() ), provided it is not canceled by a zero at dc
in the numerator
), provided it is not canceled by a zero at dc
in the numerator ![]() .
.