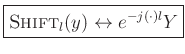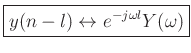Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The Shift operator is defined as
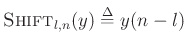 .
Since indexing is defined modulo
.
Since indexing is defined modulo 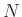 ,
,
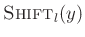 is a circular right-shift
by
is a circular right-shift
by 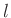 samples.
samples.
or, more loosely,
i.e.,
-
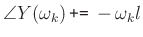
- Multiplying a spectrum
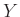 by a linear phase term
by a linear phase term
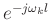 with phase slope
with phase slope 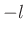 corresponds to a circular right-shift
in the time domain by
corresponds to a circular right-shift
in the time domain by 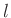 samples:
samples:
- negative slope
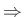 time delay
time delay
- positive slope
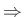 time advance
time advance
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
[Comment on this page via email]
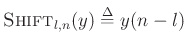 .
Since indexing is defined modulo
.
Since indexing is defined modulo 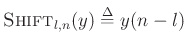 .
Since indexing is defined modulo
.
Since indexing is defined modulo ![]() ,
,
![]() is a circular right-shift
by
is a circular right-shift
by ![]() samples.
samples.