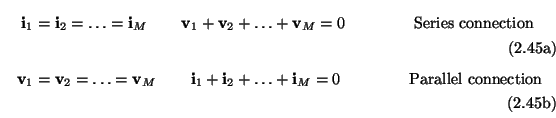Next: Coupled Inductances and Capacitances
Up: Wave Digital Elements and
Previous: Signal and Coefficient Quantization
Vector Wave Variables
It is straightforward to extend wave digital filtering principles to the vector case (this has been outlined in [131]; the same idea has apeared in the context of digital waveguide networks in [166,169]). For a 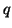 -component vector one-port element with voltage
-component vector one-port element with voltage
![$ {\bf v} = [v_{1}, \hdots, v_{q}]^{T}$](img430.png) and current
and current
![$ {\bf i} = [i_{1}, \hdots, i_{q}]^{T}$](img431.png) , it is posible to define wave variables
, it is posible to define wave variables 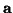 and
and 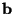 by
by
 |
(2.43a) |
for a 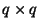 symmetric positive definite matrix
symmetric positive definite matrix 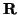 ; power-normalized quantities may be defined by
; power-normalized quantities may be defined by
 |
(2.44a) |
where
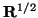 is some right square root of
is some right square root of 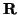 , and
, and
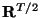 is its transpose. The power absorbed by the vector one-port will be
is its transpose. The power absorbed by the vector one-port will be
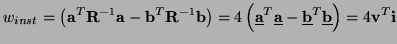 |
(2.45) |
Kirchoff's Laws, for a series or parallel connection of 
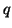 -component vector elements with voltages
-component vector elements with voltages
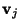 and
and
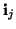 ,
,
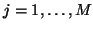 can be written as
can be written as
and the resulting scattering equations will be
in terms of the wave variables
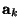 ,
,
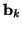 defined as per (2.43) and the port resistance matrices
defined as per (2.43) and the port resistance matrices
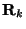 ,
,
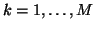 . These are the defining equations of a vector adaptor; their schematics are essentially the same as those of Figure 2.12, except that they are drawn in bold--see Figure 2.14. As before, we use the same representation for power-normalized waves.
. These are the defining equations of a vector adaptor; their schematics are essentially the same as those of Figure 2.12, except that they are drawn in bold--see Figure 2.14. As before, we use the same representation for power-normalized waves.
Figure 2.14:
Three-port vector adaptors-- (a) a vector series adaptor and (b) a vector parallel adaptor.
 |
Subsections



Next: Coupled Inductances and Capacitances
Up: Wave Digital Elements and
Previous: Signal and Coefficient Quantization
Stefan Bilbao
2002-01-22
![]()
![]() -component vector elements with voltages
-component vector elements with voltages
![]() and
and
![]() ,
,
![]() can be written as
can be written as