




Next: Stencil Width
Up: Grid Functions and Finite
Previous: Energetic Identities, Manipulations and
Contents
Index
Grid Functions and Difference Operators in Two Dimensions: Cartesian Coordinates
The extension of the definitions in §5.1.3 to two spatial coordinates is, in the Cartesian case, immediate. A grid function
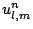 , for
, for
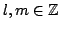 , and
, and 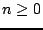 , represents an approximation to a continuous function
, represents an approximation to a continuous function 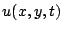 , at coordinates
, at coordinates 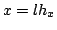 ,
, 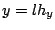 ,
, 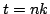 .
.
The temporal operators behave exactly as those defined in 1D, in §5.1.2, and it is not worth repeating these definitions here. Spatial shift operators, in the 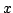 and
and 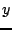 directions may be defined as
directions may be defined as
and forward, backward and centered difference operators as
Centered second derivative approximations follow immediately as
Quite important in musical sound synthesis applications is the approximation to the Laplacian operator 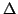 , defined as
, defined as
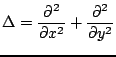 |
(5.18) |
There are many ways of approximating this operator. The simplest, by far, is to write
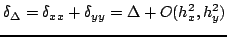 |
(5.19) |
Also important, in the case of the vibrating stiff plate, is the biharmonic operator, or bi-Laplacian, which consists of the composition of the Laplacian with itself, or
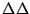 . A simple approximation may be given as
. A simple approximation may be given as
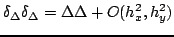 |
(5.20) |
Subsections





Next: Stencil Width
Up: Grid Functions and Finite
Previous: Energetic Identities, Manipulations and
Contents
Index
Stefan Bilbao
2006-11-15
![]() and
and ![]() directions may be defined as
directions may be defined as

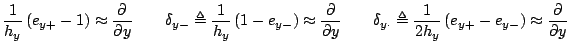
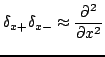
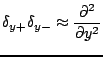
![]() , defined as
, defined as
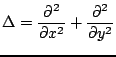
![]() . A simple approximation may be given as
. A simple approximation may be given as