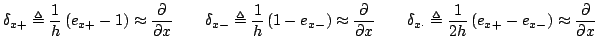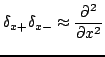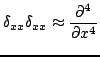Spatial Difference Operators

Approximations to spatial derivatives are based on the unit forward and backward spatial shift operations, defined as

$$e_{x+}u_{l}^{n} = u_{l+1}^{n}\qquad e_{x-}u_{l}^{n} = u_{l-1}^{n}$$

One has, immediately, the following forward, backward and centered spatial difference approximations,

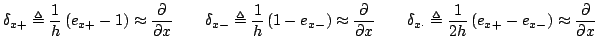$$\delta_{x+} \triangleq \frac{1}{h}\left(e_{x+}-1\right)\approx \f... ...ngleq \frac{1}{2h}\left(e_{x+}-e_{x-}\right)\approx \frac{\partial}{\partial x}$$ (5.4)

and spatial averaging operators similar to their temporal counterparts, could be defined accordingly. Simple approximations to second and fourth spatial derivatives are given by

$$\delta_{xx} = \delta_{x+}\delta_{x-}\approx\frac{\partial^2}{\partial x^2}$$ (5.5)

$$\delta_{xxxx} = \delta_{xx}\delta_{xx} \approx\frac{\partial^4}{\partial x^4}$$ (5.6)