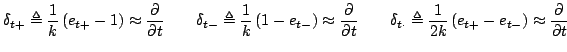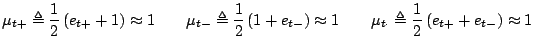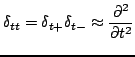Time Difference and Averaging Operators

The definitions of time difference operators in the distributed setting are nearly unchanged from those introduced in §2.2 and applied to time series. For a grid function 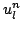$u_{l}^{n}$, the forward and backward shifts, and the identity operation ``1" are defined as

$$e_{t+}u_{l}^{n} = u_{l}^{n+1}\qquad e_{t-}u_{l}^{n} = u_{l}^{n-1}\qquad 1 u_{l}^{n} = u_{l}^{n}$$

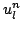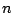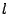and are to be regarded as applying to the time series $u_{l}^{n}$ at all values of the index $n$ and $l$. Approximations to a partial time derivative are defined as

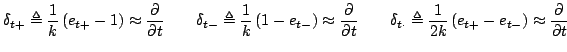$$\delta_{t+} \triangleq \frac{1}{k}\left(e_{t+}-1\right)\approx \f... ...ngleq \frac{1}{2k}\left(e_{t+}-e_{t-}\right)\approx \frac{\partial}{\partial t}$$ (5.1)

and averaging approximations to the identity operation as

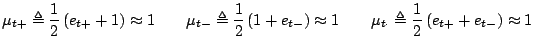$$\mu_{t+} \triangleq \frac{1}{2}\left(e_{t+}+1\right)\approx 1\qqu... ...x 1\qquad\mu_{t\cdot} \triangleq \frac{1}{2}\left(e_{t+}+e_{t-}\right)\approx 1$$ (5.2)

A simple approximation to a second time derivative is, as before,

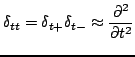$$\delta_{tt}=\delta_{t+}\delta_{t-}\approx\frac{\partial^2}{\partial t^2}$$ (5.3)