High Pass Filter Measurement

The circuit shown in Figure 7 was measured to show how the sound interface non-idealities affect a measurement. $V_{IN}$ was connected to the output of channel 1 of the PreSonus sound interface, and $V_{OUT}$ was connected to the line input of channel 1 of the interface.

Figure 7: High pass filter electrical circuit

The analog transfer function $H(f)$ can be determined analytically using the voltage divider rule:

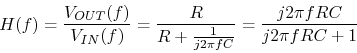$$H(f) = \frac{V_{OUT}(f)}{V_{IN}(f)} = \frac{R}{R + \frac{1}{j2\pi fC}} = \frac{j2\pi fRC}{j2\pi fRC + 1}$$ (5)

In this case, $R=1$k$\Omega$ and $C=0.47\mu$F, so the -3dB point is about $f_{3dB} = \frac{1}{2\pi RC} \approx 340$Hz. Figure 8 and Figure 9 show that the frequency response is accurately measured in the range of about 10Hz to about $9f_S/20$.

Figure 8: Measured magnitude response of the high pass filter

Figure 9: Measured phase response of the high pass filter

The ringing in the measured impulse response distracts from the more subtle characteristics of the ideal high pass filter impulse response. For transfer functions that pass large amounts of energy at high frequencies, it may be more instructive to inspect the frequency domain measurement results.

Figure 10: Impulse response