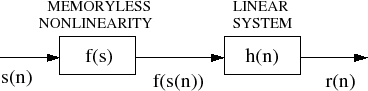 |
Mathematically, the Hammerstein system behaves as follows:
| (6) |
It turns out that we can obtain both of these desirable measurement system properties by using a
new excitation signal ![]() . This signal is a sine wave, whose frequency is
exponentially increased from
. This signal is a sine wave, whose frequency is
exponentially increased from ![]() to
to ![]() over
over ![]() seconds [2].
seconds [2].
| (7) |
where
![]() and
and
![]() . The MATLAB/Octave code
generate_sinesweeps.m
generates the appropriate sine sweep.
. The MATLAB/Octave code
generate_sinesweeps.m
generates the appropriate sine sweep.
The important property of ![]() is that the time delay
is that the time delay ![]() between any sample
between any sample ![]() and a later point with instantaneous frequency
and a later point with instantaneous frequency ![]() times larger that the instantaneous frequency at
times larger that the instantaneous frequency at ![]() is constant:
is constant:
This characteristic implies that after inverse filtering the measured response,
the signals due to the nonlinear terms in ![]() are located at specific places
in the final response signal. Consequently, the linear contribution to the response,
which is proportional to
are located at specific places
in the final response signal. Consequently, the linear contribution to the response,
which is proportional to ![]() can be separated from the other nonlinear
terms. We can thus measure a linear system even if it is being driven by a
weakly nonlinear motor.
can be separated from the other nonlinear
terms. We can thus measure a linear system even if it is being driven by a
weakly nonlinear motor.
Because the frequency of ![]() increases exponentially, the system is excited
for longer periods of time at lower frequencies. This means that the inverse
filter averages measurements at lower frequencies longer, so this measurement
technique is better suited to especially low-pass noise sources.
increases exponentially, the system is excited
for longer periods of time at lower frequencies. This means that the inverse
filter averages measurements at lower frequencies longer, so this measurement
technique is better suited to especially low-pass noise sources.