Next |
Prev |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Spectrum Analysis of Noise
Spectrum analysis of noise is generally more advanced than the
analysis of ``deterministic'' signals such as sinusoids, because the
mathematical model for noise is a so-called stochastic process,
which is defined as a sequence of random variables (see
§C.1). More broadly, the analysis of signals containing noise
falls under the subject of statistical signal processing
[121]. Appendix C provides a short tutorial on this
topic. In this chapter, we will cover only the most basic practical
aspects of spectrum analysis applied to signals regarded as noise.
In particular, we will be concerned with estimating two functions from
an observed noise sequence 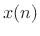 ,
,
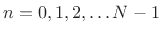 :
:
When the number 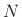 of observed samples of
of observed samples of 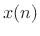 approaches infinity,
we assume that the sample autocorrelation
approaches infinity,
we assume that the sample autocorrelation
 approaches the
true autocorrelation
approaches the
true autocorrelation 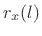 (defined formally in
Appendix C). Note that we do not need to know anything about the
true autocorrelation function--only that the sample autocorrelation
approaches it in the limit as
(defined formally in
Appendix C). Note that we do not need to know anything about the
true autocorrelation function--only that the sample autocorrelation
approaches it in the limit as
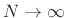 .
.
The PSD is the Fourier transform of the autocorrelation function:
 |
(7.1) |
We'll accept this as nothing more than the definition of the PSD. When
the signal 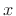 is real, both
is real, both  and
and 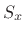 are real and even.
are real and even.
As indicated above, when estimating the true autocorrelation 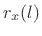 from observed samples of
from observed samples of 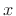 , the resulting estimate
, the resulting estimate
 will
be called a sample autocorrelation. Likewise, the Fourier
transform of a sample autocorrelation will be called a sample
PSD. It is assumed that the sample PSD
will
be called a sample autocorrelation. Likewise, the Fourier
transform of a sample autocorrelation will be called a sample
PSD. It is assumed that the sample PSD
 converges to
the true PSD
converges to
the true PSD
 as
as
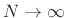 .
.
We will also be concerned with two cases of the autocorrelation
function itself:
- biased autocorrelation
- unbiased autocorrelation
The biased autocorrelation,7.1or simply
autocorrelation, will be taken to be the simplest case
computationally: If 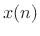 is a discrete-time signal, where
is a discrete-time signal, where 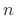 ranges
over all integers, then as described in
§2.3.7, the autocorrelation of
ranges
over all integers, then as described in
§2.3.7, the autocorrelation of 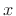 at ``lag
at ``lag 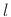 '' is given by
'' is given by
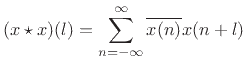 |
(7.2) |
Note that this definition of autocorrelation is workable only for
signals having finite support (nonzero over a finite number of
samples). As shown in §2.3.7, the Fourier transform of the
autocorrelation of 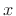 is simply the squared-magnitude of the Fourier
transform of
is simply the squared-magnitude of the Fourier
transform of 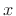 :
:
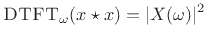 |
(7.3) |
This chapter is concerned with noise-like signals 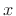 that ``last
forever'', i.e., they exhibit infinite support. As a result, we cannot
work only with
that ``last
forever'', i.e., they exhibit infinite support. As a result, we cannot
work only with 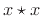 , and will introduce the unbiased
sample autocorrelation function
, and will introduce the unbiased
sample autocorrelation function
 |
(7.4) |
Since this gives an unbiased estimator of the true autocorrelation (as
will be discussed below), we see that the ``bias'' in 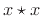 consists of a multiplication of the unbiased sample autocorrelation by
a Bartlett (triangular) window (see §3.5). This
means we can convert the biased autocorrelation to unbiased form by
simply ``dividing out'' this window:
consists of a multiplication of the unbiased sample autocorrelation by
a Bartlett (triangular) window (see §3.5). This
means we can convert the biased autocorrelation to unbiased form by
simply ``dividing out'' this window:
![$\displaystyle \hat{r}_x(l) = \left\{\begin{array}{ll} \frac{(x\star x)(l)}{N-\vert l\vert}, & \vert l\vert<N \\ [5pt] 0, & \vert l\vert\ge N \\ \end{array} \right.$](img1095.png) |
(7.5) |
Since the Fourier transform of a Bartlett window is
 (§3.5), we find that the DTFT of the biased
autocorrelation is a smoothed version of the unbiased PSD (convolved with
(§3.5), we find that the DTFT of the biased
autocorrelation is a smoothed version of the unbiased PSD (convolved with
 ).
).
To avoid terminology confusion below, remember that the
``autocorrelation'' of a signal 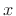 is defined here (and in
§2.3.7) to mean the maximally simplified case
is defined here (and in
§2.3.7) to mean the maximally simplified case
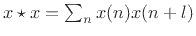 , i.e., without normalization of any kind. This definition
of ``autocorrelation'' is adopted to correspond to everyday practice
in digital signal processing. The term ``sample autocorrelation'', on
the other hand, will refer to an unbiased autocorrelation
estimate. Thus, the ``autocorrelation'' of a signal
, i.e., without normalization of any kind. This definition
of ``autocorrelation'' is adopted to correspond to everyday practice
in digital signal processing. The term ``sample autocorrelation'', on
the other hand, will refer to an unbiased autocorrelation
estimate. Thus, the ``autocorrelation'' of a signal 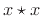 can be
viewed as a Bartlett-windowed (unbiased-)sample-autocorrelation. In the
frequency domain, the autocorrelation transforms to the
magnitude-squared Fourier transform, and the sample autocorrelation
transforms to the sample power spectral density.
can be
viewed as a Bartlett-windowed (unbiased-)sample-autocorrelation. In the
frequency domain, the autocorrelation transforms to the
magnitude-squared Fourier transform, and the sample autocorrelation
transforms to the sample power spectral density.
Subsections
Next |
Prev |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() ,
,
![]() :
:
![]() from observed samples of
from observed samples of ![]() , the resulting estimate
, the resulting estimate
![]() will
be called a sample autocorrelation. Likewise, the Fourier
transform of a sample autocorrelation will be called a sample
PSD. It is assumed that the sample PSD
will
be called a sample autocorrelation. Likewise, the Fourier
transform of a sample autocorrelation will be called a sample
PSD. It is assumed that the sample PSD
![]() converges to
the true PSD
converges to
the true PSD
![]() as
as
![]() .
.
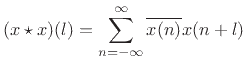
![$\displaystyle \hat{r}_x(l) = \left\{\begin{array}{ll} \frac{(x\star x)(l)}{N-\vert l\vert}, & \vert l\vert<N \\ [5pt] 0, & \vert l\vert\ge N \\ \end{array} \right.$](img1095.png)
![]() is defined here (and in
§2.3.7) to mean the maximally simplified case
is defined here (and in
§2.3.7) to mean the maximally simplified case
![]() , i.e., without normalization of any kind. This definition
of ``autocorrelation'' is adopted to correspond to everyday practice
in digital signal processing. The term ``sample autocorrelation'', on
the other hand, will refer to an unbiased autocorrelation
estimate. Thus, the ``autocorrelation'' of a signal
, i.e., without normalization of any kind. This definition
of ``autocorrelation'' is adopted to correspond to everyday practice
in digital signal processing. The term ``sample autocorrelation'', on
the other hand, will refer to an unbiased autocorrelation
estimate. Thus, the ``autocorrelation'' of a signal ![]() can be
viewed as a Bartlett-windowed (unbiased-)sample-autocorrelation. In the
frequency domain, the autocorrelation transforms to the
magnitude-squared Fourier transform, and the sample autocorrelation
transforms to the sample power spectral density.
can be
viewed as a Bartlett-windowed (unbiased-)sample-autocorrelation. In the
frequency domain, the autocorrelation transforms to the
magnitude-squared Fourier transform, and the sample autocorrelation
transforms to the sample power spectral density.