The Dolph-Chebyshev Window (or Chebyshev window, or
Dolph window) minimizes the Chebyshev norm of the side
lobes for a given main-lobe width ![]() [61,101],
[224, p. 94]:
[61,101],
[224, p. 94]:
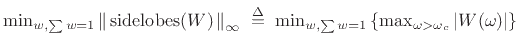 |
(4.43) |
An equivalent formulation is to minimize main-lobe width subject to a side-lobe specification:
 |
(4.44) |
The optimal Dolph-Chebyshev window transform can be written in closed form [61,101,105,156]:
![\begin{eqnarray*}
W(\omega_k) &=& \frac{\cos\left\{M\cos^{-1}\left[\beta\cos\left(\frac{\pi k}{M}\right)
\right]\right\}}{\cosh\left[M\cosh^{-1} (\beta)\right]},
\qquad k=0,1,2,\ldots,M-1 \\
\beta &=& \cosh \left[\frac{1}{M}\cosh^{-1}(10^\alpha)\right], \qquad (\alpha\approx 2,3,4).
\end{eqnarray*}](img517.png)
The zero-phase Dolph-Chebyshev window, ![]() , is then computed as the
inverse DFT of
, is then computed as the
inverse DFT of
![]() .4.14 The
.4.14 The ![]() parameter controls the side-lobe level via the formula [156]
parameter controls the side-lobe level via the formula [156]
| Side-Lobe Level in dB |
(4.45) |
The Chebyshev window can be regarded as the impulse response of an optimal Chebyshev lowpass filter having a zero-width pass-band (i.e., the main lobe consists of two ``transition bands''--see Chapter 4 regarding FIR filter design more generally).