Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
We return now to the
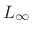 -norm minimization problem of §4.10.2:
-norm minimization problem of §4.10.2:
 |
(5.46) |
and discuss its formulation as a linear programming problem,
very similar to the optimal window formulations in §3.13.
We can rewrite (4.46) as
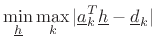 |
(5.47) |
where
 denotes the
denotes the 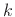 th row of the matrix
th row of the matrix
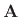 .
This can be expressed as
.
This can be expressed as
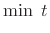 |
|
|
|
| s.t. |
|
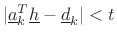 |
(5.48) |
Introducing a new variable
![$\displaystyle \tilde{{\underline{h}}} \isdefs \left[ \begin{array}{c} {\underline{h}}\\ t \end{array} \right],$](img871.png) |
(5.49) |
then we can write
![$\displaystyle t \eqsp f^T \tilde{{\underline{h}}} \isdefs \left[\begin{array}{cccc} 0 & \cdots & 0 & 1 \end{array}\right] \tilde{{\underline{h}}},$](img872.png) |
(5.50) |
and our optimization problem can be written in more standard form:
Thus, we are minimizing a linear objective, subject to a set of
linear inequality constraints.
This is known as a linear programming problem, as discussed
previously in §3.13.1, and it may be solved using the matlab
linprog function. As in the case of optimal window design,
linprog is not normally as efficient as the Remez multiple
exchange algorithm (firpm), but it is more general, allowing
for linear equality and inequality constraints to be imposed.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() -norm minimization problem of §4.10.2:
-norm minimization problem of §4.10.2:
![$\displaystyle \tilde{{\underline{h}}} \isdefs \left[ \begin{array}{c} {\underline{h}}\\ t \end{array} \right],$](img871.png)
![$\displaystyle t \eqsp f^T \tilde{{\underline{h}}} \isdefs \left[\begin{array}{cccc} 0 & \cdots & 0 & 1 \end{array}\right] \tilde{{\underline{h}}},$](img872.png)
![$\displaystyle \left\vert [\begin{array}{cc} a_k^T \; 0\\ \end{array} ] \cdot \tilde{{\underline{h}}} -{\underline{d}}_k \right\vert
\;<\; \tilde{{\underline{h}}}^T f^T\tilde{{\underline{h}}}$](img875.png)