Sampled Traveling Waves

To carry the traveling-wave solution into the ``digital domain,'' it is necessary to sample the traveling-wave amplitudes at intervals of $T$ seconds, corresponding to a sampling rate $f_s \isdeftext 1/T$ samples per second. For CD-quality audio, we have $f_s= 44.1$ kHz. The natural choice of spatial sampling interval $X$ is the distance sound propagates in one temporal sampling interval $T$ , or $X\isdeftext cT$ meters. In a lossless traveling-wave simulation, the whole wave moves left or right one spatial sample each time sample; hence, lossless simulation requires only digital delay lines. By lumping losses parsimoniously in a real acoustic model, most of the traveling-wave simulation can in fact be lossless even in a practical application.

Formally, sampling is carried out by the change of variables

$$\begin{array}{rclcl} x &\to& x_m&=& mX, \nonumber \\ t &\to& t_n&=& nT. \nonumber \end{array}$$

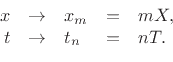
Substituting into the traveling-wave solution of the wave equation gives

$$y(t_n,x_m) \,\mathrel{\mathop=}\, y_r(t_n- x_m/c) + y_l(t_n+ x_m/c) \protect$$

$$\,\mathrel{\mathop=}\, y_r(nT- mX/c) + y_l(nT+ mX/c) \nonumber$$

$$\,\mathrel{\mathop=}\, y_r\left[(n-m)T\right]+ y_l\left[(n+m)T\right]. \protect$$

Since $T$ multiplies all arguments, let's suppress it by defining

$$y^{+}(n) \isdefs y_r(nT), \qquad\qquad y^{-}(n) \isdefs y_l(nT). \protect$$ (C.16)

This new notation also introduces a ``$+$ '' superscript to denote a traveling-wave component propagating to the right, and a ``$-$ '' superscript to denote propagation to the left. This notation is similar to that used for acoustic tubes [299].