General Series Adaptor for Force Waves

In the more general case of $N$ ports being connected in series, we have the physical constraints

$$\begin{eqnarray*} && v_1(n) = v_2(n) = \cdots = v_N(n) \isdef v_J(n)\\ && f_1(n) + f_2(n) + \cdots + f_N(n) = 0 \end{eqnarray*}$$

The derivation is the dual of that in the parallel case (cf. Eq.(F.13)), i.e., force and velocity are interchanged, and impedance and admittance are interchanged:

$$\begin{eqnarray*} 0 &=& \sum_{i=1}^N f_i \\ &=& \sum_{i=1}^NR_i\left(v^{+}_i-v^{-}_i\right)\\ &=& \sum_{i=1}^NR_i\left(2v^{+}_i-v_J\right)\\ \,\,\Rightarrow\,\,\quad \sum_{j=1}^N R_j v_J &=& \sum_{i=1}^N 2R_i v^{+}_i\\ \,\,\Rightarrow\,\,\quad v_J &=& \frac{\sum_{i=1}^N 2R_i v^{+}_i}{\sum_{j=1}^N R_j} . \end{eqnarray*}$$

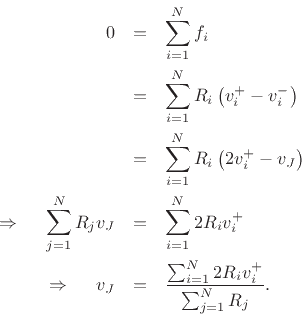
The outgoing wave variables are given by

$$v^{-}_i(n) = v_J(n) - v^{+}_i(n)$$