Delay-Line Damping Filter Design

Let $t_{60}(\omega)$ denote the desired reverberation time at radian frequency $\omega$ , and let $H_i(z)$ denote the transfer function of the lowpass filter to be placed in series with the $i$ th delay line which is $M_i$ samples long. The problem we consider now is how to design these filters to yield the desired reverberation time. We will specify an ideal amplitude response for $H_i(z)$ based on the desired reverberation time at each frequency, and then use conventional filter-design methods to obtain a low-order approximation to this ideal specification.

In accordance with Eq.(3.6), the lowpass filter $H_i(z)$ in series with a length $M_i$ delay line should approximate

$$H_i(z) = G^{M_i}(z)$$

which implies

$$\left\vert H_i(e^{j\omega T})\right\vert^{\frac{t_{60}(\omega)}{M_iT}} = 0.001.$$

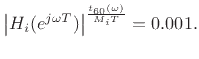
Taking $20\log_{10}$ of both sides gives

$$20 \log_{10}\left\vert H_i(e^{j\omega T})\right\vert = -60 \frac{M_i T}{t_{60}(\omega)}. \protect$$ (4.9)

This is the same formula derived by Jot [218] using a somewhat different approach.

Now that we have specified the ideal delay-line filter $H_i(e^{j\omega T})$ in terms of its amplitude response in dB, any number of filter-design methods can be used to find a low-order $H_i(z)$ which provides a good approximation to satisfying Eq.(3.9). Examples include the functions invfreqz and stmcb in Matlab. Since the variation in reverberation time is typically very smooth with respect to $\omega$ , the filters $H_i(z)$ can be very low order.