Arctangent Nonlinearity

A simple example of an invertible (one-to-one) memoryless nonlinearity is the arctangent mapping:

$$f(x) = \frac{2}{\pi}\arctan(\alpha x), \quad x\in[-1,1]$$

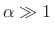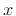where normally $\alpha\gg 1$ . This function is graphed for $\alpha=10$ in Fig.6.21. (Recall that $\arctan(x)$ is defined as the angle whose tangent is $x$ . Only angles between $-\pi /2$ and $\pi /2$ are needed to cover all real values of $x$ .)

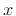Figure 6.21: Arctangent nonlinearity.