Angular Velocity Vector

When working with rotations, it is convenient to define the angular-velocity vector as a vector $\underline{\omega}\in\mathbb{R}^3$ pointing along the axis of rotation. There are two directions we could choose from, so we pick the one corresponding to the right-hand rule, i.e., when the fingers of the right hand curl in the direction of the rotation, the thumb points in the direction of the angular velocity vector.^B.18 The length $\vert\vert\,\underline{\omega}\,\vert\vert$ should obviously equal the angular velocity $\omega$ . It is convenient also to work with a unit-length variant $\underline{\tilde{\omega}}\isdeftext \underline{\omega}/ \vert\vert\,\underline{\omega}\,\vert\vert$ .

As introduced in Eq.(B.8) above, the mass moment of inertia is given by $I=mR^2$ where $R$ is the distance from the (instantaneous) axis of rotation to the mass $m$ located at $\underline{x}\in\mathbb{R}^3$ . In terms of the angular-velocity vector $\underline {\omega }$ , we can write this as (see Fig.B.6)

$$I = mR^2 \eqsp m\cdot \left\Vert\,\underline{x}-{\cal P}_{\underline{\omega}}(\underline{x})\,\right\Vert^2$$

$$= m\cdot \left\Vert\,\underline{x}-(\underline{\tilde{\omega}}^T\underline{x})\underline{\tilde{\omega}}\,\right\Vert^2 \protect$$ (B.14)

where

$${\cal P}_{\underline{\omega}}(\underline{x}) \isdefs \frac{\underline{\omega}^T\underline{x}}{\underline{\omega}^T\underline{\omega}}\underline{\omega}\eqsp (\underline{\tilde{\omega}}^T\underline{x})\underline{\tilde{\omega}}$$

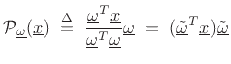
denotes the orthogonal projection of $\underline {x}$ onto $\underline {\omega }$ (or $\underline {\tilde {\omega }}$ ) [454]. Thus, we can project the mass position $\underline {x}$ onto the angular-velocity vector $\underline {\omega }$ and subtract to get the component of $\underline {x}$ that is orthogonal to $\underline {\omega }$ , and the length of that difference vector is the distance to the rotation axis $R$ , as shown in Fig.B.6.

Figure B.6: Mass position vector $\underline {x}$ and its orthogonal projection ${\cal P}_{\protect\underline{\omega}}(\underline{x})$ onto the angular velocity vector $\underline {\omega }$ for purposes of finding the distance $R$ of the mass $m$ from the axis of rotation $\underline {\tilde {\omega }}$ .

Using the vector cross product (defined in the next section), we will show (in §B.4.17) that $R$ can be written more succinctly as

$$R \eqsp \left\Vert\,\underline{x}-{\cal P}_{\underline{\omega}}(\underline{x})\,\right\Vert \eqsp \left\Vert\,\underline{\tilde{\omega}}\times \underline{x}\,\right\Vert.$$