Transposed Direct-Forms

The remaining two direct forms are obtained by formally transposing direct-forms I and II [60, p. 155]. Filter transposition may also be called flow graph reversal, and transposing a Single-Input, Single-Output (SISO) filter does not alter its transfer function. This fact can be derived as a consequence of Mason's gain formula for signal flow graphs [49,50] or Tellegen's theorem (which implies that an LTI signal flow graph is interreciprocal with its transpose) [60, pp. 176-177]. Transposition of filters in state-space form is discussed in §G.5.

The transpose of a SISO digital filter is quite straightforward to find: Reverse the direction of all signal paths, and make obviously necessary accommodations. ``Obviously necessary accommodations'' include changing signal branch-points to summers, and summers to branch-points. Also, after this operation, the input signal, normally drawn on the left of the signal flow graph, will be on the right, and the output on the left. To renormalize the layout, the whole diagram is usually left-right flipped.

Figure 9.3 shows the Transposed-Direct-Form-I (TDF-I) structure for the general second-order IIR digital filter, and Fig.9.4 shows the Transposed-Direct-Form-II (TDF-II) structure. To facilitate comparison of the transposed with the original, the input and output signals remain ``switched'', so that signals generally flow right-to-left instead of the usual left-to-right. (Exercise: Derive forms TDF-I/II by transposing the DF-I/II structures shown in Figures 9.1 and 9.2.)

Figure: Transposed-Direct-Form-I implementation of a second-order IIR digital filter. Note that the input signal comes in from the right, and the output is on the left. Compare to Fig.9.1. The four ``state variable'' signals are labeled arbitrarily as $s_1(n)$ through $s_4(n)$ .

Figure: Transposed-Direct-Form-II implementation of a second-order IIR digital filter (input on the right, output on the left). Compare to Fig.9.2.

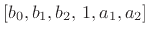The difference equation implementing TDF-II can be written by inspection from Fig.9.4:

$$\begin{eqnarray*} y(n) &=& s_1(n) + b_0 x(n)\\ s_1(n+1) &=& s_2(n) + b_1 x(n) - a_1 y(n)\\ s_2(n+1) &=& b_2 x(n) - a_2 y(n) \end{eqnarray*}$$

Using this update order, no temporary storage elements are required, i.e., $s_1$ is updated after it is used, using $s_2$ , and then $s_2$ is updated.

We can refer to $s_1(n)$ and $s_2(n)$ the state of the filter at time $n$ . It is typical in state-space formulations to label delay-element outputs as state variables, and write update equations for the state at time $n+1$ as we have done here. See Appendix G for more about state-space formulations.