|
The Computer Polyrhythmicon page 3 of 4 |
Selected Works |
|
The Computer Polyrhythmicon page 3 of 4 |
Selected Works |
Rend for snare drum quartet and polyrhythmicon/bass drum explores the transformational properties of noise and dense polyrhythmic counterpoint. Noise (chaos) is gradually reordered into a precise polyrhythmic system (order) which is then generationally transformed into new systems. The layers of polyrhythmic activity, continually transforming into relational rhythmic sets, originate and terminate in noise. The computer performer plays the polyrhythmicon, controlling a snare drum program on a sampler or synthesizer. In Rend, the polyrhythmicon is treated as a hyper-instrument, augmenting the rhythmic potential of the human percussionists by extending an elemental rhythmic system into densely packed polyrhythmic fields. The snare drum provides an ideal instrument for a piece of this nature because the timbre is noisy and the instrument is capable of precise rhythmic placement. The snare drums create fields of noise as well as simple polyrhythms while the polyrhythmicon, taking advantage of the computers precision and speed accomplishes the transformation from noise into more complex polyrhythms.
The piece begins with a simple three-voice polyrhythm emerging from colored noise 3:5:7. Using the polyrhythmicon this transformation from noise to rhythm was accomplished by programming each module to its maximal tempo setting with slight displacement of beats between voices. Snare drum sounds played in this manner create the illusion of a continuous noise signal. By slowly adjusting each voice to align again in phase, the illusion of pulse emerging from noise was created.
While the percussionists play the relatively simple polyrhythms 3:5:7 and 6:11:14, the computer expands the polyrhythmic system towards greater complexity. The outer voices move exponentially from 3:7 to 6:14 to 9:21. These proportionally stable polyrhythms in the outer voices create a sense of rhythmo-harmonic stability. The inner voice progresses in prime numbers from 5 to 11 to 13. 7 is left out of the progression because it is part of the original 3:5:7 polyrhythm. The prime motion gives the entire system a sense of instability characterized by the relation of the prime number to the outer voices.
Once the basic 3:5:7 polyrhythm was established it again transforms along fixed trajectories. The outer voices, 3 and 7, traverse an exponential curve from 3 to 6 and 7 to 14. The inner voice moves linearly to the next unused prime number, 11. The system then accelerates similarly to the next stage, 9 : 13 : 21. Again the outer voices move exponentially and the inner voice moves to the next prime number. The final transformation accelerates the voices beyond the point of rhythmic differentiation and back into noise.

|
|
|
Rhythmic form of Rend
This process is then reversed. The polyrhythmicon retraces the path from noise to 9:13:21 to 6:11:14 to 3:5:7 and into silence. Simultaneously the snare drums disintegrate from a unison into a gradually accelerating polyrhythmic field which eventually ends in noise. The percussion and computer working simultaneously in opposite structural directions form an interesting contradiction which resolves in the circular nature of the original form: from noise, to rhythm, to noise. Rend transverses musical parameters in the sense that structurally it oscillates between timbre and rhythm. In this case timbre is an absolute structural state: noise. Rhythm on the other hand is fluid and dynamic. Rend introduced the concept of a dynamic interplay between timbral and rhythmic devices to my work. This idea came to fruition in Symphony in Metal, discussed later in this document.

|
|
|
 |
|
|
|
" a dense thicket of rhythm that seems to pulsate, sometimes at regular intervals, sometimes at startling intervals that seem rhythmically dissonant as Burtner modulates the pattern." Dale Keiger, Johns Hopkins Magazine |
Taruyamaarutet: Twisted Faces (in wood) for soprano, marimba, bass clarinet, percussion, polyrhythmicon/electronics, movement artist, and projected images focuses on a different aspect of rhythm/pitch relationship. Rather than concentrating solely on macro-timbral relationships, rhythm is treated as a functional system with an internal hierarchical structure. Traditional techniques of functional pitch systems are applied to the rhythmic domain and control large scale form. In this way I studied rhythmic gesture as an independent system of structural ordering. Each section of the piece utilizes a different rhythmic form to create unity and structural motion. The concept of harmonic-rhythm, developed by Henry Cowell (Cowell 1930, 1961, 1978) is the conceptual basis behind the realization of the work. At the crux of this interpretation of Cowells theories is the concept that, similar to harmony, rhythm is functional and can exhibit degrees of consonance and dissonance in the same way as harmony. Simple, integer-based ratios such as 2:3 exhibit a high degree of periodicity or consonance. Fractional ratios and more complex integer ratios such as 17:31.13 are more aperiodic or dissonant.
|
" Taruyamaarutet draws on knowledge of orchestral instruments and computer wizardry, taking advantage of the computer's precision to make complicated sequences of sounds that no human could possibly master." Eillen Murphy, Baltimore City Paper |
In Taruyamaarutet, a single four voice polyrhythm, 6:8:9:12, is used throughout the piece as the tonic rhythm. This polyrhythm was chosen for its characteristic sound brought about by what I have termed its nested polyrhythm status. A nested polyrhythm is a polyrhythmic set formed of more than one polyrhythmic subset which are proportional to one another in a different ratio. In this case, for example, 6 is to 8 as 9 is to 12both, when reduced, are in a 3:4 ratio. In addition, (6:8) and (9:12) are in a 2:3 ratio against one another. This combination of nested polyrhythms creates a highly characteristic, easily recognizable sound.

|
|
|

|
|
|

|
|
|

|
| Polyrhythmic Layers of the Computer Solo |
The rhythmic function occurs when this tonic rhythm can be established in the ear of the listener and then transformed into a new recognizable form. The first section is in the form of a rondo, an alternation between a returning theme and new material such as the song form A B A C A. This rhythmic rondo is accomplished by gradually speeding up and slowing down each voice independently until it becomes another voice in the progression. Between measures 7 and 10 the original 6:8:9:12 rhythm transforms into 8:9:12:6. The rhythm becomes a revoiced version of itself. This cyclic process continues until the original voicing returns and the section ends. The transformational material between the tonic polyrhythm is the new material while the tonic polyrhythm returns in between in a slightly changed form. The form of this section then is A B A1 C A2 D A3 E A.
The second section (mm4676) utilizes augmentation as a formal device. In this case, augmentation refers to a process whereby the original rhythm is gradually constructed by adding voices one at a time. Rather than stay in only four voices the original four voice motive is augmented to 6 voices6 : 8 : 9 : 12 : 16 : 18. The nested polyrhythm is extended from a two subset system to three subsets, the last subset being an octave extension of the first in that 6:12, 8:16, and 9:18 are all in a 1:2 ratio.
In the third section of Taruyamaarutet, modulation is accomplished by moving from the original polyrhythm through a more dissonant set, 5:11:7:17, and ending on a closely related set 3:15:4:20. The closely related polyrhythm, 3:15:4:20 is also a nested polyrhythm, composed of two 3:4 (3:4 and 15:20) ratios related in a 1:5 proportion ((3:15) : (4:20)). This new polyrhythm is analogous to the dominant set, and is treated as a dominant harmonic area throughout the piece. The dissonant polyrhythm was created by identifying a highly characteristic area of the transformational space between the two nested polyrhythms. Once identified, the rhythm was agogically stressed to bring it to prominence.
In the most rhythmically intense moment of the piece, the computer solo (m144), three layers of polyrhythmic activity take place simultaneously. The first layer is a very dissonant polyrhythmic set, 15:17.5:20:27.5 (gradually constructed in the preceding measures, 124-135), playing only the accents on every 6th, 8th, 9th, and 12th notes of the respective voice. The second layer is a repetitive rhythmic transformational loop in which a rhythm of 3:4:9:12:15:20 changes into 9:15:12:20:6:8 and then back, in the time of about 1.3 seconds. The third layer is a heavy drumming polyrhythm composed of the dominant set, 3:15:4:20. These three layers occur simultaneously for about 25 seconds and the listener has a chance to bask in the chaos of this dense polyrhythmic fabric.
Taruyamaarutet attempts to fathom the possibilities of rhythmic functionality. While the piece utilizes an abstract arbitrary system of functional organization, other forms of functionality can be derived from natural sonorous systems. Timbre provides an ideal model for a functional musical system as it is based on one such natural system. Spectral composition has shown that new harmonic systems can be successfully generated from timbral structures (McAdams/Saariaho 1985; Saariaho 1985, 1987) . Symphony in Metal, for large orchestra and electronics provides one such system.

|
|
|

|
|
|
|
|

|

|

|
Rhythmically, Symphony in Metal represents a further integration of rhythmic micro and macro structuring by mapping timbral frequency relationships into the rhythmic domain. Polyrhythmic changes in the work reflect timbral juxtapositions. The title in Metal refers to the materialization of sound extended multiparametrically into other elements of the work. Spectral information, frequency and amplitude of formant structures, and the relationship between them is transposed into the rhythmic domain by shifting the absolute relationships of FFT data down into a range where it is no longer perceived as frequency but is heard as rhythmic material (c. 1/8Hz18Hz) (Stockhausen 1961). When applied in this way, the musical material itself becomes the compositional algorithm.
Timbre, perceived as a single sound, in reality is formed of many discreet frequency elements (Moore 1992). Color also is made of discreet parts that blend congruently in our perception. Mapping timbral microstructure into the rhythmic domain is similar to spreading the spectrum of a color into its primary components so that the relationship of each can be perceived. By slowing down the relationships in this manner, a significant integration of micro and macro structure can be achieved. In particular, the timbral structure of the work depends on poles of change from soft metal (flute) to harsh metal (brass) to true metal (metal objects) to electronic distortion (increased distortion of spectrographic image of metal) to noise. The change in timbral form takes place fluidly and freely defining areas of dissonance and consonance.
The rhythmic structure is based on a transformational polyrhythmic system modeling the timbral changes in the work, and a nested polyrhythmic set similar to that used in Taruyamaarutet.. The derived set, initiated in the low strings at the opening of the work, is the point of rhythmic origin of the work. This polyrhythm, (5:3) : (3:3) : (5:4) : (3:4), forms two proportional rhythms, [ (5:3) : (3:3) ] : [ (5:4) : (3:4) ], which are together in a ratio of 3 : 4.
The nested polyrhythm is juxtaposed with a transformational spectrographic rhythmic structure. To generate this second rhythmic system, spectral analysis and resynthesis of a tuba low F building from pianissimo to fortissimo, and a single anvil attack were used. The two sounds were spectrally morphed by establishing the trajectory of spectral displacement of the tuba sound as it became richer in upper partials and projecting that displacement towards the even richer spectral components of the anvil attack. The resulting spectral analysis reveals a path of timbral transformation between the two.
Once the spectral data was created, a series of analyses were generated in order to produce a variety of output information. One such analysis became the formal idea out of which the harmonic material was created. Another, non-graphical analysis was used to compose the rhythmic system.
Associating rhythmic voices with formant regions common to both sounds, a group of abstract polyrhythmic changes was generated. The spectrographic rhythmic material is used freely throughout but it appears most notably in the cadenza for percussion and electronics beginning the second half of the work. The material transforms slowly as the strength of upper partials gradually increases and additional, more dissonant rhythmic voices, are added to mirror the timbral trajectories of the modeled sounds. This mapping of spectral data from an acoustic sound source could be done in real time by sampling a live instrument, analyzing the recorded file and resynthesizing it on the polyrhythmicon, and further work will need to be done to implement this performance method.
Once the polyrhythmic set representing the tuba/anvil spectrum has been created, the polyrhythms begin to slightly distort and become abstracted from their spectral origins. The penultimate rhythm is chaos, a wild rush of stochastically generated rhythmic pulses coinciding with the introduction of acoustical noise and the high string melody of the final section. An in depth analysis of the other musical elements in the piece can be found in my paper, Rhythm Noise and Space (Burtner 1997).
The synthesis of spectrally generated polyrhythmic systems in order to form a solid integration of micro and macro sound structure creates new possibilities for rhythm to function as a prime motivator of musical structure. The potential for this technique is far reaching and further study will be necessary. In this application, the polyrhythmicon becomes less of a hyper-instrument and more of a means of resynthesizing analysis files. Symphony in Metal makes extensive progress towards creating an effective way of working in this manner.
|
||
|
|

|
|
|
|
|
|
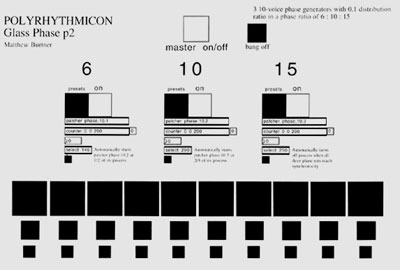
Glass Phase (1998) explores structures of rhythmic and spectrographic transformation of glass sounds. In the first section of the piece a polymetric technique is used in which three voices in single-unit differentiated tempo-phase relationships (such as 21:22:23) contain a nested polyrhythmic phase structure utilizing meter-phase (such as accents on beats 7, 8 and 9 of each respective voice). Several of these "linked polymetric sets" are used in conjunction, each new set fading in and out independently. In the second section large scale "phase sets" are created from 10 voices offset by 1/100th of a rhythmic pulse. The result is an expanding and contracting rhythmic structure. Several of these phase sets are used simultaneously in a macro-polyrhythmic relationship of 6 : 10 : 15 [(3 : 5) : (2 : 3)]. Glass Phase was composed during a composer residency at the Phonos Foundation / Audiovisual Institute in Barcelona, Spain.

|
|
|
| Ê |
SOUND EXAMPLE: GLASS PHASE.mp3 |
Stone Phase explores form as a function of dynamic polyrhythmic phase systems. Polyrhythmic stone textures containing as many as 32 independent transforming tempi are hierarchically ordered by phase relationships to create slowly evolving polyrhythmic systems. Largely ordered into two sections, the piece moves from the disorder of the initial stone explosion, through processes of hierarchical rhythmic organization, finally into a unified, in phase pulse.
The first section is based on an inversion of temporal and metrical order. An initial 8 voice polyrhythm (3:4:5:6:7:8:9:10) gradually accelerates to fifteen times its original speed. As the system accelerates, accents on the 15th beat of each voice are introduced creating a very slow polymeter between the voices. The metric system, being linked to the accelerating tempi, also accelerates. As the polymetric structure approaches the speed of the initial polytempo, it begins to supplant the microrhythm and the listener is left at the beginning of the rhythmic cycle: the original tempo. In this section a dynamic form is established between micro and macro rhythmic structure. The point at which the resultant meter becomes the original tempo represents a structural convergence point and begins the second section.
Moving concurrently, in contrary temporal motion to the accelerating stones, a low pulse undergoes a process of deceleration. The eight stone voices and the low pulse in this section exhibit no internal rhythmic relationship but work against one another. In the second section they join together. Additionally, the stone voices are not in phase and therefore do achieve internal convergence points between all voices at any time. Rather the entrances are dovetailed.
The second section begins with the initial tempo of the first section but with the 8 voice polyrhythm in phase with itself. At the convergence point of system A, a second 8 voice system (system B) enters at a tempo ratio of 4/3 of system A. At the convergence point of system B, a third 8 voice group (system C) enters at a tempo of 4/3 tempo B. Similarly a fourth system begins at the convergence point of system C at 4/3 the ratio of that tempo. The result of this system is that after four repetitions of each phase group, all 4 systems (32 voices) come into phase on one downbeat. At this point all four groups begin to accelerate independently. Each system exhibits internal temporal similarity but the acceleration curves of the four systems are different. The systems are guided by a single, fixed tempo-point in the future and so each group moves independently to reach that point at the appropriate time. As the large convergence point approaches the systems begin to come into phase and the aural result is of some sort of order attempting to arise from the disorder.
Throughout this section, low attacks accentuate the convergence points of each system. Each system has its own low pitched attack. As the section progresses the low pulses begin a spacial trajectory outward filling the stereo field. The envelope of each attack is also altered and as the 4 systems come into phase, the four low attacks become a swooshing pulse (revealing how the low pulses in the first section were created). The low pulses and stone systems come into phase on a single convergence point.
This point of structural convergence represented a compositional problem because while the rhythmic problem had been solved, the musical energy was unresolved. An extended coda follows section B in which the residue of the amassed energy is diffused and other musical timbral issues are resolved such as the high sounds and noise which permeate the piece and are independent of the stone rhythms.
| SOUND EXAMPLE: STONE PHASE.mp3 |
PREVIOUS PAGE: The Polyrhythmicon || NEXT PAGE: Resources / Contact
©Matthew Burtner 1997-2000, All rights reserved