picture(4674,4674)(889,-4423)
(2258,-1898)(0,0)[lb]
|

picture(4674,4674)(889,-4423)
(2258,-1898)(0,0)[lb]
|
In order to simulate the boundary with the wells of different depths
in a 2-D digital waveguide mesh, we need to convert the depths of the
wells in Equation 4 to the number of
junctions. Since the travel time of the wave in the ![]() th well is
given by
th well is
given by
where ![]() is the depth of the
is the depth of the ![]() th well, and
th well, and ![]() is the speed of
the sound, we can calculate the travel time in samples for the
traveling wave by multiplying Equation 10 by the
sampling rate, i.e.,
is the speed of
the sound, we can calculate the travel time in samples for the
traveling wave by multiplying Equation 10 by the
sampling rate, i.e.,
where ![]() is the travel time in samples in the
is the travel time in samples in the ![]() th well and
th well and ![]() is the sampling rate. Substituting
is the sampling rate. Substituting ![]() with that in Equation
4 yields
with that in Equation
4 yields
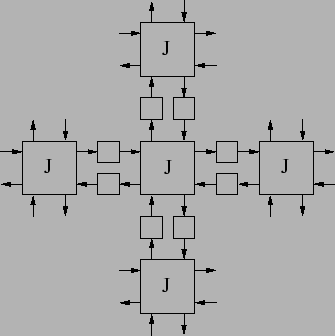
Since the wells are rigidly separated from each other in Schroeder's diffuser, we need to take this into account when implementing it in a 2-D digital waveguide mesh. This can be accomplished by disconnecting all the horizontal strings between adjacent junctions in the wells as shown in Figure 4. The disconnection of the strings between junctions means the junctions in the wells are no more considered 4-port junctions, and this changes the scattering coefficients. In fact, the junctions in the wells are now pure digital delay lines without any scattering, having reflections only at the end of the wells. The junctions are terminated at the boundaries with a reflection coefficient of 0.99.
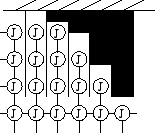 |
The design wavelength ![]() used in our simulation is 25
used in our simulation is 25 ![]() ,
and each well is one sample wide, which gives the well width of
,
and each well is one sample wide, which gives the well width of
![]() . Therefore, the
. Therefore, the
![]() requirement in Schroeder's diffuser has been satisfied.
requirement in Schroeder's diffuser has been satisfied.