Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
In the second simulations we fix the bow position to 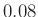 , where 0
represents the bridge while 1 represents the nut, and we vary bow
velocity and bow force.
, where 0
represents the bridge while 1 represents the nut, and we vary bow
velocity and bow force.
Subsections
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download stiffbowed.pdf
Download stiffbowed_2up.pdf
Download stiffbowed_4up.pdf
![]() , where 0
represents the bridge while 1 represents the nut, and we vary bow
velocity and bow force.
, where 0
represents the bridge while 1 represents the nut, and we vary bow
velocity and bow force.