Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
where
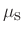 =coefficient of static friction
=coefficient of static friction
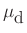 =coefficient of dynamic friction
=coefficient of dynamic friction
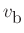 =bow velocity
=bow velocity
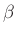 =bow position
=bow position
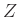 =characteristic impedance of the string,
=characteristic impedance of the string,
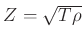
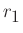 =term that represents losses of the string
=term that represents losses of the string
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download stiffbowed.pdf
Download stiffbowed_2up.pdf
Download stiffbowed_4up.pdf