Zero padding consists of extending a signal (or spectrum)
with zeros. It maps a length ![]() signal to a length
signal to a length ![]() signal, but
signal, but
![]() need not divide
need not divide ![]() .
.
Definition:
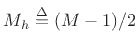 for
for
In this example, the first sample corresponds to time 0, and five zeros have been inserted between the samples corresponding to times
Figure 7.7 illustrates zero padding from length ![]() out to length
out to length
![]() . Note that
. Note that ![]() and
and ![]() could be replaced by
could be replaced by ![]() and
and ![]() in the
figure caption.
in the
figure caption.
![\includegraphics[width=\twidth]{eps/zpad}](img1222.png) |
Note that we have unified the time-domain and frequency-domain
definitions of zero-padding by interpreting the original time axis
![]() as indexing positive-time samples from 0
to
as indexing positive-time samples from 0
to
![]() (for
(for ![]() even), and negative times in the interval
even), and negative times in the interval
![]() .7.9 Furthermore, we require
.7.9 Furthermore, we require
![]() when
when ![]() is even, while odd
is even, while odd ![]() requires no such
restriction. In practice, we often prefer to interpret time-domain
samples as extending from 0
to
requires no such
restriction. In practice, we often prefer to interpret time-domain
samples as extending from 0
to ![]() , i.e., with no negative-time
samples. For this case, we define ``causal zero padding'' as
described below.
, i.e., with no negative-time
samples. For this case, we define ``causal zero padding'' as
described below.