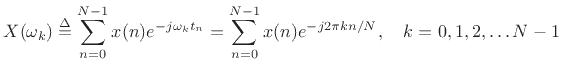Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
For a length  complex sequence
complex sequence 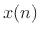 ,
,
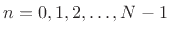 , the
discrete Fourier transform (DFT) is defined by
, the
discrete Fourier transform (DFT) is defined by
We are now in a position to have a full understanding of the transform kernel:
The kernel consists of samples of a complex sinusoid at  discrete
frequencies
discrete
frequencies 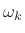 uniformly spaced between 0
and the sampling
rate
uniformly spaced between 0
and the sampling
rate
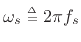 . All that remains is to understand
the purpose and function of the summation over
. All that remains is to understand
the purpose and function of the summation over  of the pointwise
product of
of the pointwise
product of 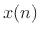 times each complex sinusoid. We will learn that
this can be interpreted as an inner product operation which
computes the coefficient of projection of the signal
times each complex sinusoid. We will learn that
this can be interpreted as an inner product operation which
computes the coefficient of projection of the signal 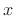 onto
the complex sinusoid
onto
the complex sinusoid
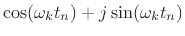 . As
such,
. As
such,
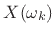 , the DFT at frequency
, the DFT at frequency 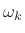 , is a measure of
the amplitude and phase of the complex sinusoid which is present in
the input signal
, is a measure of
the amplitude and phase of the complex sinusoid which is present in
the input signal 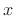 at that frequency. This is the basic function of
all linear transform summations (in discrete time) and integrals (in
continuous time) and their kernels.
at that frequency. This is the basic function of
all linear transform summations (in discrete time) and integrals (in
continuous time) and their kernels.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() complex sequence
complex sequence ![]() ,
,
![]() , the
discrete Fourier transform (DFT) is defined by
, the
discrete Fourier transform (DFT) is defined by