Convolution (cyclic or acyclic) is commutative, i.e.,
Proof:
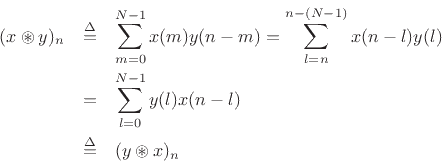
In the first step we made the change of summation variable
![]() , and in the second step, we made use of the fact
that any sum over all
, and in the second step, we made use of the fact
that any sum over all ![]() terms is equivalent to a sum from 0
to
terms is equivalent to a sum from 0
to
![]() .
.